题目内容
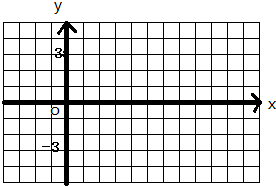 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x-| π |
| 3 |
(1)在给定的平面直角坐标系中,利用五点法画函数f(x)=3sin(2x-
| π |
| 3 |
(2)求f(x)=3sin(2x-
| π |
| 3 |
(3)若方程f(x)=m在[-
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由条件利用五点法做函数函数y=3sin(2x-
)在一个周期上的简图.
(2)根据正弦函数的定义域和值域,令2kπ-
≤2x-
≤2kπ+
,k∈z,求得x的范围,可得函数f(x)的增区间.
(3)由题意可得,函数y=f(x)的图象和直线y=m在[-
,0]上有交点.由x∈[-
,0],利用正弦函数的定义域和值域求得f(x)的范围,即为m的范围.
| π |
| 3 |
(2)根据正弦函数的定义域和值域,令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
(3)由题意可得,函数y=f(x)的图象和直线y=m在[-
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)列表:
∵x∈[0,π],∴2x-
∈[-
,
],
作图: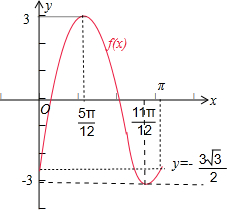
(2)令2kπ-
≤2x-
≤2kπ+
,k∈z,求得 kπ-
≤x≤kπ+
,
故函数f(x)的增区间为[kπ-
,kπ+
],k∈z.
再结合x∈[-π,0],可得函数的增区间为[-π,-
]、[-
,0].
(3)∵方程f(x)=m在[-
,0]上有实根,∴函数y=f(x)的图象和直线y=m在[-
,0]上有交点.
由x∈[-
,0]可得,2x-
∈[-
,-
],sin(2x-
)∈[-1,
],f(x)∈[-3,
].
故m的取值范围为[-3,
].
∵x∈[0,π],∴2x-
| π |
| 3 |
| π |
| 3 |
| 5π |
| 3 |
2x-
| -
| 0 |
| π |
|
| ||||||||||
| x | 0 |
|
|
|
| π | ||||||||||
| f(x) | -
| 0 | 3 | 0 | -3 | -
|

(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
故函数f(x)的增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
再结合x∈[-π,0],可得函数的增区间为[-π,-
| 7π |
| 12 |
| π |
| 12 |
(3)∵方程f(x)=m在[-
| π |
| 2 |
| π |
| 2 |
由x∈[-
| π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
故m的取值范围为[-3,
3
| ||
| 2 |
点评:本题主要考查用五点法做函数函数y=Asin(ωx+φ)在一个周期上的简图,正弦函数的单调性,正弦函数的定义域和值域,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
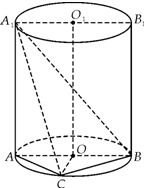 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°. 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=