题目内容
求下列直线与双曲线的交点坐标：
（1）2x-y-10=0，
-
=1；
（2）4x-3y-16=0，
-
=1．
（1）2x-y-10=0，
| x2 |
| 20 |
| y2 |
| 5 |
（2）4x-3y-16=0，
| x2 |
| 25 |
| y2 |
| 16 |
考点：双曲线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：将直线方程和双曲线方程联立，消去y，整理可得x的方程，运用解二次方程的方法，即可求得交点坐标．
解答：
解：（1）由
消去y，得3x2-32x+84=0，解得x=6或
，
由x=6可得y=2，由x=
可得y=-
，即有交点坐标为（6，2），（
，-
）；
（2）由
消去y，得16x2-200x+625=0，解得x1=x2=
．
求得y1=y2=3，即有交点坐标为（
，3）．
|
| 14 |
| 3 |
由x=6可得y=2，由x=
| 14 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 2 |
| 3 |
（2）由
|
| 25 |
| 4 |
求得y1=y2=3，即有交点坐标为（
| 25 |
| 4 |
点评：本题考查双曲线的方程，主要考查联立直线方程和双曲线方程，消去一个未知数，解方程求交点，考查运算能力，属于基础题．
练习册系列答案
相关题目
某厂对一批产品进行了抽样检测，如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）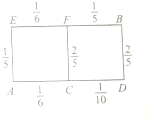
某物流公司送货员从公司A处准备开车送货到某单位B处，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图所示（例如A→C→D算作两个路段：路段AC发生堵车事件的概率为