题目内容
已知向量
,
均为单位向量,它们的夹角为600,实数x,y满足|x
+y
|=
,那么x+2y的最大值为( )
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
考点:平面向量数量积的运算
专题:等差数列与等比数列
分析:向量
,
均为单位向量,它们的夹角为600,可得|
|=|
|=1,
•
=1×1×cos60°=
.由|x
+y
|=
,可得x2+y2+xy=3,设x+2y=t,则x=t-2y,可得3y2-3ty+t2-3=0,利用△≥0,解出即可.
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 3 |
解答:
解:∵向量
,
均为单位向量,它们的夹角为600,
∴|
|=|
|=1,
•
=1×1×cos60°=
.
∵|x
+y
|=
,
∴
=
,
化为x2+y2+xy=3,
设x+2y=t,则x=t-2y,
∴(t-2y)2+y2+(t-2y)y=3,
化为3y2-3ty+t2-3=0,
∵y∈R,
∴△=9t2-12(t2-3)≥0,
解得|t|≤2
,
∴t即x+2y的最大值为2
.
故选:C.
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| 1 |
| 2 |
∵|x
| a |
| b |
| 3 |
∴
x2+y2+2xy×
|
| 3 |
化为x2+y2+xy=3,
设x+2y=t,则x=t-2y,
∴(t-2y)2+y2+(t-2y)y=3,
化为3y2-3ty+t2-3=0,
∵y∈R,
∴△=9t2-12(t2-3)≥0,
解得|t|≤2
| 3 |
∴t即x+2y的最大值为2
| 3 |
故选:C.
点评:本题考查了向量的数量积定义及其运算性质、一元二次方程有实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,则三棱锥P-ABC的体积为( )
| A、21π | ||||
| B、12π | ||||
C、
| ||||
D、
|
若一个三棱锥有三个面两两垂直,则称此三棱锥为直角三棱锥,在长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中,正确的是( )
A、若|
| ||||||||||||||
B、若
| ||||||||||||||
C、若(
| ||||||||||||||
D、若
|
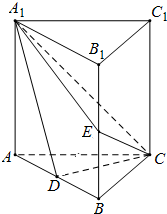 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= 某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )