题目内容

若f（x）=f（x+2），当x∈[-1，1]时f（x）=1-x2，则当x∈[1，3]时，f（x）=
 
．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：将在x属于[-1，1]时的f（x）=1-x2中的x换为（x+2）即可．
解答： 解：∵f（x）=f（x+2），f（x）=1-x2，
∴f（x+2）=1-（x+2）2=-x2-4x-3．
点评：本题考查了函数的周期性，函数解析式的求法，是一道基础题．
练习册系列答案
相关题目
讨论函数f（x）=x2-2ax+3在（-2，2）内的单调性．
求函数y=
4a2+x2
+
(x-a)2+a2
的最小值（a＞0）．
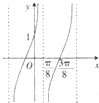已知函数f（x）=Atan（ωx+φ）（ω＞0，|φ|＜
π
2
），y=f（x）的部分图象如图所示，若f（x0）=
3
，则x0等于（　　）
A、
π
24
B、
kπ
2
+
π
24
，k∈Z
C、kπ+
π
3
，k∈Z
D、
Kπ
2
+
π
3
，k∈Z
已知函数f（x）=-x3+x2+b，g（x）=alnx
（1）若f（x）在x∈[-
1
2
，1）上的最大值为
3
8
，求实数b的值；
（2）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求实数a的取值范围．
是否存在实数a，c，使函数f（x）=
ax+1
x2+c
的值域为[1，5]，若存在，求出a，c的值；若不存在，请说明理由．
二面角α-l-β中，平面α的一个法向量n1=（
3
2
，-
1
2
，-
2
），平面β的一个法向量n2=（0，
1
2
，
2
]，则二面角α-l-β的大小为（　　）
A、120°
B、150°
C、30°或150°
D、60°或120°
函数f（x）=log 
1
2
（x+x-4）的零点所在的区间为
 
．
求函数y=（1+2x-3x2）3的导数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网