题目内容
5. 如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;
如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;(2)求平面ADE与平面ACF所成锐二面角的大小.
分析 (1)若M为AE的中点,根据线面平行的判定定理即可证明EC∥平面BDM;
(2)根据二面角的定义作出二面角的平面角,结合三角形的边角关系即可求平面ADE与平面ACF所成锐二面角的大小.
解答  (1)证明连接:设AC交BD于P,连接PM.
(1)证明连接:设AC交BD于P,连接PM.
三角形ACE中,M为AE中点,P为AC中点,
∴CE∥PM.
∵PM?平面BDM中,CM?平面BDM中,
∴CE∥平面BDM.
(2)延长CF和DE交于G,连接AG.作三角形AG边上的高DN,连接CN
∵CD⊥AD,CD⊥DG,
∴CD⊥平面ADG,
∵AG?平面ADG,故CD⊥AG.
∵DN⊥AG,
∴AG⊥平面CDN.
则CN⊥AG.
则∠CND是二面角的平面角
∵EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.
∴DG=2,AG=$\sqrt{6}$.
∵sin∠DGN=$\frac{DN}{DG}=\frac{AD}{AG}$,
∴DN=$\frac{2\sqrt{3}}{3}$.
则tan∠CND=$\frac{CD}{DN}$=$\sqrt{3}$,
故∠CND=60°.
即平面ADE与平面ACF所成锐二面角的大小60°.
点评 本题主要考查空间线面平行的判断以及二面角的求解,根据相应的定理以及二面角平面角的定义作出二面角的平面角是解决本题的关键.本题也可以建立空间直角坐标系,利用向量法进行求解.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
14.设x>0,则y=3-2x-$\frac{1}{x}$的最大值为( )
| A. | 3 | B. | 3-3$\sqrt{2}$ | C. | 3-2$\sqrt{3}$ | D. | -1 |
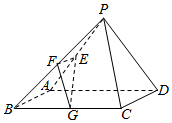 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点. 一几何体的三视图如图所示
一几何体的三视图如图所示