题目内容
14.已知直线l1:ax+y+1=0(a>0)与直线l2:x+(b-4)y+2=0(b>0)垂直,则a2+b2的最小值为8.分析 由直线垂直可得b=4-a,且0<a<4,代入并变形可得a2+b2=2a2-8a+16,由二次函数的最值可得.
解答 解:∵直线l1:ax+y+1=0(a>0)与直线l2:x+(b-4)y+2=0(b>0)垂直,
∴a•1+1•b-4=0,即正数a、b满足a+b=4,∴b=4-a,
又b=4-a>0可得a<4,综合可得0<a<4,
∴a2+b2=a2+(4-a)2=2a2-8a+16,
∴当a=-$\frac{-8}{2×2}$=2时,上式取最小值8,
故答案为:8.
点评 本题考查直线的一般式方程和垂直关系,涉及二次函数求最值,属基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2.对任意非零实数a,b,若a?b的运算原理如图所示,则20.5?log0.5$\frac{1}{4}$的值为( )
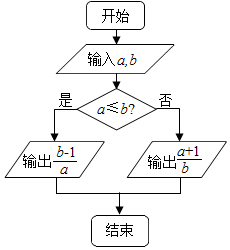

| A. | $\frac{{\sqrt{2}+1}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}-1}}{2}$ |
9.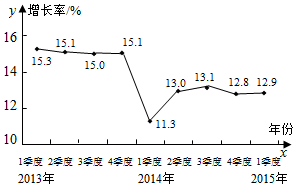 如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
 如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )| A. | 近三年该市生产总值为负增长 | |
| B. | 近三年该市生产总值为正增长 | |
| C. | 该市生产总值2013年到2014年为负增长,2014年到2015年为正增长 | |
| D. | 以上判断都不正确 |
3.执行如图所示的程序框图,则该程序运行后输出的i值为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
4.在数列{an}中,“|an+1|>an”是“数列{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;
如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;