题目内容
10.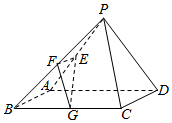 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.(Ⅰ)求证:EF⊥平面PAD;(Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小;
(Ⅲ)线段PD上是否存在一个动点M,使得直线GM与平面EFG所成角为$\frac{π}{6}$,若存在,求线段PM的长度,若不存在,说明理由.
分析 (Ⅰ)根据线面垂直的判定定理即可证明EF⊥平面PAD;
(Ⅱ)建立坐标系,求出平面的法向量,利用向量法即可求平面EFG与平面ABCD所成锐二面角的大小;
(Ⅲ)求出向量坐标,利用直线和平面所成角的定义和关系进行求解即可.
解答 (Ⅰ)证明:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD
∴AB⊥平面PAD,(2分)
又∵EF∥AB∴EF⊥平面PAD,(3分)
(Ⅱ)取AD中点O,连结PO∵平面PAD⊥平面ABCD,
PO⊥AD∴PO⊥平面ABCD,(4分)
如图以O点为原点分别以OG、OD、OP所在直线为x轴y轴z轴建立空间直角坐标系:
∴O(0,0,0)A(0,-2,0)B(4,-2,0)C(4,2,0),
D(0,2,0),G(4,0,0),$P(0,0,2\sqrt{3})$,E(0,-1,$\sqrt{3}$)$F(2,-1,\sqrt{3})$$\overrightarrow{EF}=(2,0,0),\overrightarrow{EG}=(4,1,-\sqrt{3})$,
设平面EFG的法向量为$\overrightarrow m=(x,y,z)$,$\left\{{\begin{array}{l}{2x=0}\\{4x+y-\sqrt{3}z=0}\end{array}}\right.$,
∴$\overrightarrow m=(0,\sqrt{3},1)$,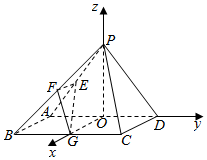 (6分)
(6分)
又平面ABCD的法向量为$\overrightarrow n=(0,0,1)$,(7分)
设平面EFG与平面ABCD所成锐二面角为θ∴$cosθ=\frac{{|{\overrightarrow{m•}\overrightarrow n}|}}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{1}{2}$,
∴平面EFG与平面ABCD所成锐二面角为$\frac{π}{3}$.(9分)
(Ⅲ)设$\overrightarrow{PM}=λ\overrightarrow{PD},λ∈[{0,1}]$,$\overrightarrow{GM}=\overrightarrow{GP}+\overrightarrow{PM}=\overrightarrow{GP}+λ\overrightarrow{PD}$,
∴$\overrightarrow{GM}=(-4,2λ,2\sqrt{3}(1-λ))$,(10分),
∴$sin\frac{π}{6}=|{cos\left?{\overrightarrow{GM},\overrightarrow m}\right>}|=\frac{{|{\overrightarrow{GM}•\overrightarrow m}|}}{{|{\overrightarrow{GM}}|•|{\overrightarrow m}|}}$=$\frac{{2\sqrt{3}}}{{2\sqrt{16+4{λ^2}+12{{(1-λ)}^2}}}}=\frac{1}{2}$,(12分)
即2λ2-3λ+2=0,无解,∴不存在这样的M.(13分)
点评 本题主要考查空间面面垂直的判定以及二面角和线面角的求解,建立空间坐标系,求出平面的法向量,利用向量法是解决本题的关键.

| A. | 220 | B. | 110 | C. | 55 | D. | 100 |
| A. | 1 | B. | -1 | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |

| A. | [0,7] | B. | [0,4] | C. | [1,7] | D. | [1,4] |
| A. | $\frac{{\sqrt{2}+1}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}-1}}{2}$ |
 如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;
如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;