题目内容
11.已知在数列{an}中,a1=1,an+1-2an•an+1-an=0,求数列{an}的通项公式.分析 讨论可知an≠0,从而化简可得$\frac{1}{{a}_{n}}$-2-$\frac{1}{{a}_{n+1}}$=0,从而判断出{$\frac{1}{{a}_{n}}$}是以1为首项,-2为公差的等差数列,再求an.
解答 解:∵an+1-2an•an+1-an=0,
∴an+1(1-2an)=an,
又∵a1=1≠0,∴an≠0,
∴$\frac{1}{{a}_{n}}$-2-$\frac{1}{{a}_{n+1}}$=0,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-2,
∴{$\frac{1}{{a}_{n}}$}是以1为首项,-2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1-2(n-1)=3-2n,
故an=$\frac{1}{3-2n}$.
点评 本题考查了构造法求解数列的通项公式的应用及转化思想的应用.

练习册系列答案
相关题目
16.己知函数f(x)=$\left\{\begin{array}{l}{cos\frac{π}{4}x,x≤2000}\\{x-14,x>2000}\end{array}\right.$,则f[f(2014)]=( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |
2.对任意非零实数a,b,若a?b的运算原理如图所示,则20.5?log0.5$\frac{1}{4}$的值为( )
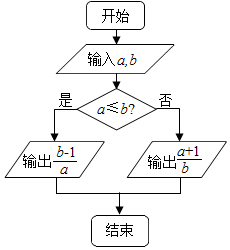

| A. | $\frac{{\sqrt{2}+1}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}-1}}{2}$ |
3.执行如图所示的程序框图,则该程序运行后输出的i值为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
 如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;
如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;