题目内容
函数y=|x+2|-|x-2|的最小值为 .
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:利用绝对值的几何意义,分类讨论,即可求出函数的最小值.
解答:
解:x<-2时,y=-4;
-2≤x≤2时,y=2x∈[-4,4];
x>2时,y=4,
∴函数y=|x+2|-|x-2|的最小值为-4.
故答案为:-4.
-2≤x≤2时,y=2x∈[-4,4];
x>2时,y=4,
∴函数y=|x+2|-|x-2|的最小值为-4.
故答案为:-4.
点评:本题考查函数的最值及其几何意义,正确分类讨论是关键.

练习册系列答案
相关题目
下列函数中,周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(2x+
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(2x-
|
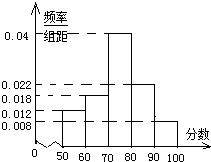 某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.
某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.