题目内容
已知|
|=1，|
|=
．
（Ⅰ）若
与
的夹角为60°，求|
+
|；
（Ⅱ）若
-
与
垂直，求
与
的夹角．
| a |
| b |
| 2 |
（Ⅰ）若
| a |
| b |
| a |
| b |
（Ⅱ）若
| a |
| b |
| a |
| a |
| b |
考点：数量积表示两个向量的夹角,向量的模
专题：平面向量及应用
分析：（Ⅰ）由题意可得
•
=
，再根据|
+
|=
=
，计算求得结果．
（Ⅱ）若
-
与
垂直，则有（
-
）•
=0，由此求得cos＜
，
＞的值，可得
与
的夹角．
| a |
| b |
| 2 |
| a |
| b |
(
|
|
（Ⅱ）若
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
解答：
解：（Ⅰ）若
与
的夹角为60°，则有
•
=|
|•|
|cos60°=
，
∴|
+
|=
=
=
=
+1．
（Ⅱ）若
-
与
垂直，则有（
-
）•
=
2-
•
=1-1×
×cos＜
，
＞=0，
由此求得cos＜
，
＞=
，∴
与
的夹角为
．
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
∴|
| a |
| b |
(
|
|
1+2+2
|
| 2 |
（Ⅱ）若
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| a |
| b |
| 2 |
| a |
| b |
由此求得cos＜
| a |
| b |
| ||
| 2 |
| a |
| b |
| π |
| 4 |
点评：本题主要考查用两个向量的数量积表示两个向量的夹角，两个向量的数量积的定义，两个向量垂直的性质，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
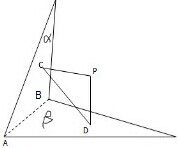已知P是二面角α-AB-β内一点，PC⊥α，垂足为C，PD⊥β，垂足为D，且PC=3，PD=4，∠CPD=60°，求：