题目内容
有编号为1、2、3、4、5的五道不同的政治题和编号为6、7、8、9的四道不同的历史题,一位同学从这九道题中任意抽取两道,每道题被抽中的机会相等.
(1)共有多少种不同的抽取结果;
(2)求这位同学抽取的两道题编号之和小于17但不小于11的概率.
(1)共有多少种不同的抽取结果;
(2)求这位同学抽取的两道题编号之和小于17但不小于11的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)从九道题中任意抽取两道,共有
种方法
(2)计算出求这位同学抽取的两道题编号之和小于17但不小于11的基本事件个数,代入古典概型概率计算公式,可得答案.
| C | 2 9 |
(2)计算出求这位同学抽取的两道题编号之和小于17但不小于11的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)∵有编号为1、2、3、4、5的五道不同的政治题和编号为6、7、8、9的四道不同的历史题,
从这九道题中任意抽取两道,共有
=
=36(种)方法,(或8+7+6+5+4+3+2+1=36种)…6分
(2)设抽取的两道题编号之和小于17但不小于11为事件A,
事件包括以下15个基本事件:
(9,7)、(9,6)、(9,5)、(9,4)、(9,3)、
(9,2)、(8,7)、(8,6)、(8,5)、(8,4)、
(8,3)、(7,6)、(7,5)、(7,4)、(6,5),
所以P(A)=
=
…(12分)
从这九道题中任意抽取两道,共有
| C | 2 9 |
| 9×8 |
| 2 |
(2)设抽取的两道题编号之和小于17但不小于11为事件A,
事件包括以下15个基本事件:
(9,7)、(9,6)、(9,5)、(9,4)、(9,3)、
(9,2)、(8,7)、(8,6)、(8,5)、(8,4)、
(8,3)、(7,6)、(7,5)、(7,4)、(6,5),
所以P(A)=
| 15 |
| 36 |
| 5 |
| 6 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
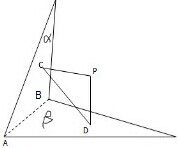 已知P是二面角α-AB-β内一点,PC⊥α,垂足为C,PD⊥β,垂足为D,且PC=3,PD=4,∠CPD=60°,求:
已知P是二面角α-AB-β内一点,PC⊥α,垂足为C,PD⊥β,垂足为D,且PC=3,PD=4,∠CPD=60°,求: