题目内容
已知等比数列{an}中,a5+2a4=a2a4,前2m(m∈N*)项和是前2m项中所有偶数项和的
倍.
(Ⅰ)求通项an;
(Ⅱ)已知{bn}满足bn=(n-λ)an(n∈N*),若{bn}是递增数列,求实数λ的取值范围.
| 3 |
| 2 |
(Ⅰ)求通项an;
(Ⅱ)已知{bn}满足bn=(n-λ)an(n∈N*),若{bn}是递增数列,求实数λ的取值范围.
考点:等比数列的性质,数列与函数的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用前2m(m∈N*)项和是前2m项中所有偶数项和的
倍,求出公比,利用a5+2a4=a2a4,求出a1,即可求通项an;
(Ⅱ)利用
=
>1,即可求实数λ的取值范围.
| 3 |
| 2 |
(Ⅱ)利用
| bn+1 |
| bn |
| 2(n+1-λ) |
| n-λ |
解答:
解:(Ⅰ)设公比为q,则
∵前2m(m∈N*)项和是前2m项中所有偶数项和的
倍,
∴
=
•
,
∴q=2,
∵等比数列{an}中,a5+2a4=a2a4,
∴a1q4+2a1q3=a1q•a1q3,
∴a1=2,
∴an=2n;
(Ⅱ)bn=(n-λ)2n,则
=
>1,
∴λ<n,
∴λ≤1.
∵前2m(m∈N*)项和是前2m项中所有偶数项和的
| 3 |
| 2 |
∴
| a1(1-q2m) |
| 1-q |
| 3 |
| 2 |
| a1q[1-(q2)m] |
| 1-q2 |
∴q=2,
∵等比数列{an}中,a5+2a4=a2a4,
∴a1q4+2a1q3=a1q•a1q3,
∴a1=2,
∴an=2n;
(Ⅱ)bn=(n-λ)2n,则
| bn+1 |
| bn |
| 2(n+1-λ) |
| n-λ |
∴λ<n,
∴λ≤1.
点评:本题考查等比数列的通项与求和,考查学生的计算能力,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
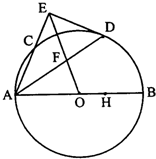 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F. 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆O的切线l,则点A到直线l的距离AD=
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆O的切线l,则点A到直线l的距离AD=