题目内容
已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＜f（x）g′（x），f（x）=axg（x），
+
=
，则
=（ ）
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 10 |
| 3 |
| f(2) |
| g(2) |
| A、a2 | ||
B、
| ||
| C、9 | ||
D、
|
考点：函数的单调性与导数的关系
专题：导数的概念及应用
分析：根据函数的单调性和导数之间的关系求出a的值，即可得到结论．
解答：
解：∵f（x）=axg（x），
∴
=ax，
∵f′（x）g（x）＜f（x）g′（x），
∴[
]′=
＜0，
即函数
=ax，单调递减，即0＜a＜1．
又
+
=
，
则a+
=
，解得a=
或a=3（舍去）．
即
=(
)x，
∴
=(
)2=
，
故选：D．
∴
| f(x) |
| g(x) |
∵f′（x）g（x）＜f（x）g′（x），
∴[
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
即函数
| f(x) |
| g(x) |
又
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 10 |
| 3 |
则a+
| 1 |
| a |
| 10 |
| 3 |
| 1 |
| 3 |
即
| f(x) |
| g(x) |
| 1 |
| 3 |
∴
| f(2) |
| g(2) |
| 1 |
| 3 |
| 1 |
| 9 |
故选：D．
点评：本题主要考查指数函数的性质，利用导数研究函数的单调性，求出a的值是解决本题的关键．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
| 10 |
| 3 |
| 14 |
| 7 |
| A、＞ | B、≥ | C、≤ | D、＜ |
设函数f（x）=|lnx|，则下列结论中正确的是（ ）
A、f（1）＜f（
| ||
B、f（
| ||
C、f（e）＜f（1）＜f（
| ||
D、f（e）＜f（
|
设ab＞0，下面四个不等式中，正确的是（ ）
①|a+b|＞|a|；②|a+b|＜|b|；③|a+b|＜|a-b|；④|a+b|＞|a|-|b|
①|a+b|＞|a|；②|a+b|＜|b|；③|a+b|＜|a-b|；④|a+b|＞|a|-|b|
| A、①和② | B、①和③ |
| C、①和④ | D、②和④ |
过点A（2，b）和点B（3，-2）的直线的倾斜角为
，则b的值是（ ）
| 3π |
| 4 |
| A、-1 | B、1 | C、-5 | D、5 |
关于x的不等式ax2+2ax-4＜0对一切x∈R恒成立，则a的取值范围是（ ）
| A、（-4，0） |
| B、（-4，0] |
| C、[-4，0） |
| D、[-4，0] |
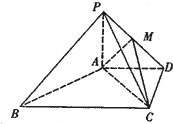如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，PB⊥AC，AD⊥CD，且AD=CD=2