题目内容
已知圆E与x轴相切,圆心在y轴正半轴上,且被直线x-y=0截得的弦长为2
.
(1)求圆E 标准方程;
(2)过定点P(-3,0)的直线交圆E于不同的两点M,N,在线段MN上取异于M,N的点H(x0,y0),满足
=
,试求点H的横坐标x0的取值范围.
| 2 |
(1)求圆E 标准方程;
(2)过定点P(-3,0)的直线交圆E于不同的两点M,N,在线段MN上取异于M,N的点H(x0,y0),满足
|
| ||
|
|
|
| ||
|
|
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)求出圆心到直线x-y=0的距离,即可求出b,从而可得圆E标准方程;
(2)由已知直线MN的斜率一定存在,设为k,则其方程为y=kx+3k,联立方程消去y,P,M,H,N四点共线,将四点都投影到x轴上,则
=
,可转化为
=
,求出x0=-
=-3+
,即可求点H的横坐标x0的取值范围.
(2)由已知直线MN的斜率一定存在,设为k,则其方程为y=kx+3k,联立方程消去y,P,M,H,N四点共线,将四点都投影到x轴上,则
|
| ||
|
|
|
| ||
|
|
| x1+3 |
| x2+3 |
| x0-x1 |
| x2-x0 |
| 6k |
| 2k+3 |
| 9 |
| 2k+3 |
解答:
解:(1)由已知可设圆E的圆心(0,b),则半径为b.
∵圆心到直线x-y=0的距离d=
=
,
解得b2=4,b=-2(舍去),b=2,
∴圆E的标准方程为x2+(y-2)2=4.
(2)设M(x1,y1),N(x2,y2),H(x0,y0),
由已知直线MN的斜率一定存在,设为k,则其方程为y=kx+3k,
联立方程消去y,得(1+k2)x2+2k(3k-2)x+(3k-2)2-4=0,
于是x1+x2=-
,x1x2=
.①
又P,M,H,N四点共线,将四点都投影到x轴上,
则
=
,可转化为
=
,
将①代入整理得:x0=-
=-3+
,
由
<2,可解得0<k<
,
于是可得-
<x0<0,满足-2<x0<2,
∴-
<x0<0.
∵圆心到直线x-y=0的距离d=
b2-(
|
| |b| | ||
|
解得b2=4,b=-2(舍去),b=2,
∴圆E的标准方程为x2+(y-2)2=4.
(2)设M(x1,y1),N(x2,y2),H(x0,y0),
由已知直线MN的斜率一定存在,设为k,则其方程为y=kx+3k,
联立方程消去y,得(1+k2)x2+2k(3k-2)x+(3k-2)2-4=0,
于是x1+x2=-
| 2k(3k-2) |
| 1+k2 |
| (3k-2)2-4 |
| 1+k2 |
又P,M,H,N四点共线,将四点都投影到x轴上,
则
|
| ||
|
|
|
| ||
|
|
| x1+3 |
| x2+3 |
| x0-x1 |
| x2-x0 |
将①代入整理得:x0=-
| 6k |
| 2k+3 |
| 9 |
| 2k+3 |
由
| |-2+3k| | ||
|
| 12 |
| 5 |
于是可得-
| 24 |
| 13 |
∴-
| 24 |
| 13 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在△ABC中,设角A,B,C的对边分别为a,b,c.已知B=45°,C=120°,b=2,则c=( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
在区间[-2,3]中任取一个数m,则“方程
+
=1表示焦点在x轴上的椭圆”的概率是( )
| x2 |
| m+3 |
| y2 |
| m2+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为
如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为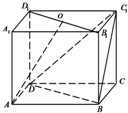 如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证:
如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证: