题目内容
若抛物线y=ax2的焦点与双曲线
-x2=1的焦点重合,则a的值为 .
| y2 |
| 3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的焦点,即为抛物线的焦点,将抛物线方程化为标准方程,即可得到焦点坐标,解方程可得a.
解答:
解:双曲线
-x2=1的a=
,b=1,c=
=2,
则焦点为(0,±2),
抛物线y=ax2即为x2=
y的焦点为(0,
),
由题意可得,
=±2,
解得,a=±
.
故答案为:±
.
| y2 |
| 3 |
| 3 |
| 3+1 |
则焦点为(0,±2),
抛物线y=ax2即为x2=
| 1 |
| a |
| 1 |
| 4a |
由题意可得,
| 1 |
| 4a |
解得,a=±
| 1 |
| 8 |
故答案为:±
| 1 |
| 8 |
点评:本题考查抛物线和双曲线的方程和性质,考查运算能力,属于基础题和易错题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
运行如图所示的程序框图,则输出的结果S为( )


| A、2014 | B、2013 |
| C、1008 | D、1007 |
如图所示,程序框图(算法流程图)的输出结果是( )
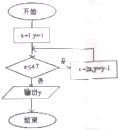

| A、0 | B、-1 | C、-2 | D、-3 |
一个几何体的三视图如图所示,则该几何体的体积为( )
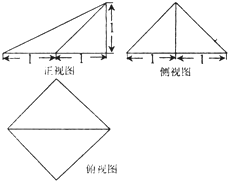

| A、2 | ||
B、
| ||
C、
| ||
D、
|
