题目内容
在平面直角坐标系中，O为原点．A（0，sinα），B（2cosα，0），动点C满足|
|=1，|
+
+
|的最大值是（ ）
| AC |
| OA |
| OB |
| OC |
| A、9 | B、8 | C、4 | D、3 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于动点C满足|
|=1，所以C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），利用向量模的平方等于向量的平方，将|
+
+
|2写成关于θ的三角函数解析式，利用余弦函数的有界性求最值．
| AC |
| OA |
| OB |
| OC |
解答：
解：∵|
|=1，
∴C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），
∴|
+
+
|2=（2cosα+cosθ）2+（sinα+sinθ+sinα）2=sin2θ+cos2θ+4cosαcosθ+4sinαsinθ+4=4cos（α-θ）+5≤9，
∴原式最大值为3；
故选：D．
| AC |
∴C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），
∴|
| OA |
| OB |
| OC |
∴原式最大值为3；
故选：D．
点评：本题考查了向量的模与向量的平方相等以及利用三角函数的有界性求最值，属于中档题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
运行如图所示的程序框图，则输出的结果S为（ ）
| A、2014 | B、2013 |
| C、1008 | D、1007 |
下列命题错误的是（ ）
| A、已知直线a∥b，且b∥c，则a∥c |
| B、已知直线a∥平面α，且直线b∥平面α，则a∥b |
| C、已知直线a∥平面α，过平面α内一点作b∥a，则b?α |
| D、过平面外一点可以做无数条直线与这个平面平行，并且这些直线都在同一平面内 |
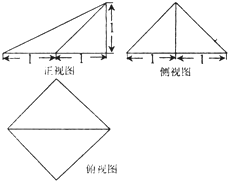
一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、2 | ||
B、
| ||
C、
| ||
D、
|
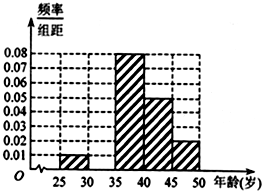某市要对辖区内的中学教师的年龄进行调查，现从中随机抽出200名教师，已知抽到的教师年龄都在[25，50）岁之间，根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是（ ）