题目内容
在区间[-2,3]中任取一个数m,则“方程
+
=1表示焦点在x轴上的椭圆”的概率是( )
| x2 |
| m+3 |
| y2 |
| m2+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:椭圆的标准方程,列举法计算基本事件数及事件发生的概率
专题:圆锥曲线的定义、性质与方程,概率与统计
分析:表示焦点在x轴上的椭圆,则m+3>m2+1,可得区间长度,求出在区间[-2,3]上随机取一个实数m的区间长度,即可得出结论.
解答:
解:∵方程
+
=1表示焦点在x轴上的椭圆,
∴m+3>m2+1,
解得-1<m<2,
故概率P=
=
故选:A
| x2 |
| m+3 |
| y2 |
| m2+1 |
∴m+3>m2+1,
解得-1<m<2,
故概率P=
| 2-(-1) |
| 3-(-2) |
| 3 |
| 5 |
故选:A
点评:本题考查概率的求法,是较基础题,解题时要认真审题,注意几何概型的合理运用.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )
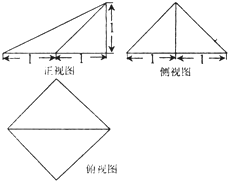

| A、2 | ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的离心率是( )
| x2 |
| 2 |
| y2 |
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50
,则抛物线的方程为( )
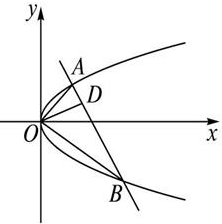
| 5 |

| A、y2=20x | ||
| B、y2=10x | ||
| C、y2=5x | ||
D、y2=
|
已知实数x,y满足不等式组
,则2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、9 |
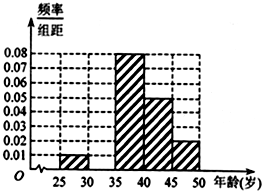 某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )
某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )