题目内容
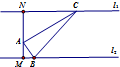 如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,
如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,| AB |
| cos∠ABC |
| AC |
| cos∠ACB |
①△ABC是直角三角形;
②
| 1 |
| AB |
| 2 |
| AC |
| 2 |
③(S四边形MBCN)min=(S△ABC)min+(S△AMB+S△ACN)min;
④设△AMB的周长为y1,△ACN的周长为y2,则(y1+y2)min=10.
考点:正弦定理
专题:解三角形
分析:①由正弦定理得:
=
=
,则可求得sin2C=sin2B,进而根据∵AB≠AC,进而求得A+B的值,则A的值可求得.
②设∠BAM=θ(0<θ<
),则可分别表示出∠CNA,AB,AC,MB,CN,
则
+
可表示出来,利用两角和公式整理后利用三角函数性质求得其最大值;
③分别运用θ表示出四边形MBCN,和三角形ABC的面积利用基本不等式求得其最小值;
用θ表示出y1+y2,令t=tan
(0<t<1),进而利用二次函数的性质求得其最小值.
| AB |
| AC |
| sinC |
| sinB |
| cosB |
| cosC |
②设∠BAM=θ(0<θ<
| π |
| 2 |
则
| 1 |
| AB |
| 2 |
| AC |
③分别运用θ表示出四边形MBCN,和三角形ABC的面积利用基本不等式求得其最小值;
用θ表示出y1+y2,令t=tan
| θ |
| 2 |
解答:
解:①由正弦定理得:
=
=
,则sin2C=sin2B,又∵AB≠AC,∴B+C=
,A=
,
所以①正确;
②设∠BAM=θ(0<θ<
),则∠CAN=
-θ,AB=
,AC=
,MB=tanθ,CN=2cotθ,
则
+
=sinθ+cosθ=
sin(θ+
),(
+
)max=
,所以②正确;
③S四边形MBCN=
(tanθ+2cotθ)≥3
,S△ABC=
≥2S△AMB+S△ACN=
(4cotθ+tanθ)≥2,所以③错误;
④y1+y2=3+
+
=3+
+
,
令t=tan
(0<t<1),y1+y2=3+
+
≥10(当t=
时取等),所以④正确.
故答案为:①②④
| AB |
| AC |
| sinC |
| sinB |
| cosB |
| cosC |
| π |
| 2 |
| π |
| 2 |
所以①正确;
②设∠BAM=θ(0<θ<
| π |
| 2 |
| π |
| 2 |
| 1 |
| cosθ |
| 2 |
| sinθ |
则
| 1 |
| AB |
| 2 |
| AC |
| 2 |
| π |
| 4 |
| 1 |
| AB |
| 2 |
| AC |
| 2 |
③S四边形MBCN=
| 3 |
| 2 |
| 2 |
| 2 |
| sin2θ |
| 1 |
| 2 |
④y1+y2=3+
| 1+sinθ |
| cosθ |
| 2(1+cosθ) |
| sinθ |
sin
| ||||
cos
|
2cos
| ||
sin
|
令t=tan
| θ |
| 2 |
| t+1 |
| 1-t |
| 2 |
| t |
| 1 |
| 2 |
故答案为:①②④
点评:本题主要考查了正弦定理的应用,两角和公式的应用,函数思想以及转化与化归思想的运用.

练习册系列答案
相关题目
已知x∈R,则“x<0”是“x<cosx”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图是某班甲乙两同学高三各次联考的数学成绩的茎叶图.根据统计学知识判断甲、乙两同学中发挥较稳定的是
如图是某班甲乙两同学高三各次联考的数学成绩的茎叶图.根据统计学知识判断甲、乙两同学中发挥较稳定的是