题目内容
已知x∈R,则“x<0”是“x<cosx”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义,利用数形结合,即可得到结论.
解答:
 解:作出函数y=x,与y=cosx的图象,当x<0时,x<cosx成立,即充分性成立.
解:作出函数y=x,与y=cosx的图象,当x<0时,x<cosx成立,即充分性成立.
若当x=0时,满足x<cosx但x<0不成立,即必要性不成立,
故“x<0”是“x<cosx”的充分不必要条件,
故选:A.
 解:作出函数y=x,与y=cosx的图象,当x<0时,x<cosx成立,即充分性成立.
解:作出函数y=x,与y=cosx的图象,当x<0时,x<cosx成立,即充分性成立.若当x=0时,满足x<cosx但x<0不成立,即必要性不成立,
故“x<0”是“x<cosx”的充分不必要条件,
故选:A.
点评:本题主要考查充分条件和必要条件的应用,利用数形结合是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图程序运行后,输出的值是( )


| A、9 | B、-4 | C、14 | D、5 |
设0<x<
,记a=lnsinx,b=sinx,c=esinx,则比较a,b,c的大小关系为( )
| π |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、b<c<a |
由函数y=cosx与x=0,x=
π,y=0围成的几何图形的面积为( )
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若(x+2i)•i=y-2i,x,y∈R,则复数x+yi=( )
| A、-2-2i | B、1+2i |
| C、2+i | D、2+2i |
若函数f(x)为偶函数,x>0时,f(x)单调递增,P=f(-π),Q=f(e),R=f(
),则P,Q,R的大小为( )
| 2 |
| A、R>Q>P |
| B、P>Q>R |
| C、P>R>Q |
| D、Q>R>P |
在△ABC中,∠C=90°,P为三角形内一点且S△PAB=S△PBC=S△PCA,则
=( )
| PA2+PB2 |
| PC2 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、5 |
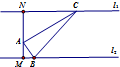 如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,
如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,