题目内容
若存在实常数k和b,使得函数f(x)和g(x)对其定义域内的任意实数x分别满足f(x)≥kx+b和g(x)≤kx+b,则称直线l:y=kx+b为f(x)和g(x)的“分界直线”.已知函数f(x)=2x2-4和函数g(x)=4lnx-2,那么函数f(x)和函数g(x)的分界直线方程为 .
考点:导数在最大值、最小值问题中的应用
专题:新定义,导数的综合应用
分析:令F(x)=f(x)-g(x)=2x2-4-4lnx+2=2x2-2-4lnx(x>0),利用导数可求得F(x)的最小值是0及两图象的公共点(1,-2),从而可判断f(x)和g(x)的分界直线过这个公共点,则分界线可表示为y=kx-k-2,由f(x)≥kx-k-2恒成立可求得k值,再证明g(x)≤4x-6在x>0时恒成立即可,利用导数易证.
解答:
解:令F(x)=f(x)-g(x)=2x2-4-4lnx+2=2x2-2-4lnx(x>0),
∴F′(x)=4x-
=
,令F′(x)=0,得x=1,
当0<x<1时,F′(x)<0,x>1时,F′(x)>0,
故当x=1时,F(x)取到最小值,最小值是0,
∴函数f(x)和g(x)的图象在(1,-2)处相交,
因此存在f(x)和g(x)的分界直线,那么该直线过这个公共点,
则-2=k+b,即y=kx-k-2,
由f(x)≥kx-k-2(x∈R),可得2x2-kx+k-2≥0当x∈R恒成立,
则△=k2-8k+16=(k-4)2≤0,
∴k=4,此时直线方程为:y=4x-6.
下面证明g(x)≤4x-6在x>0时恒成立,
令G(x)=g(x)-(4x-6)=4lnx-4x+4(x>0),
则G′(x)=
-4=
,
则当0<x<1时G′(x)>0,G(x)递增;当x>1时G′(x)<0,G(x)递减;
则当x=1时,G(x)取到极大值,极大值是0,也是最大值.
∴G(x)=g(x)-(4x-6)≤0,则g(x)≤4x-6当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的分界直线y=4x-6.
∴F′(x)=4x-
| 4 |
| x |
| 4(x+1)(x-1) |
| x |
当0<x<1时,F′(x)<0,x>1时,F′(x)>0,
故当x=1时,F(x)取到最小值,最小值是0,
∴函数f(x)和g(x)的图象在(1,-2)处相交,
因此存在f(x)和g(x)的分界直线,那么该直线过这个公共点,
则-2=k+b,即y=kx-k-2,
由f(x)≥kx-k-2(x∈R),可得2x2-kx+k-2≥0当x∈R恒成立,
则△=k2-8k+16=(k-4)2≤0,
∴k=4,此时直线方程为:y=4x-6.
下面证明g(x)≤4x-6在x>0时恒成立,
令G(x)=g(x)-(4x-6)=4lnx-4x+4(x>0),
则G′(x)=
| 4 |
| x |
| 4(1-x) |
| x |
则当0<x<1时G′(x)>0,G(x)递增;当x>1时G′(x)<0,G(x)递减;
则当x=1时,G(x)取到极大值,极大值是0,也是最大值.
∴G(x)=g(x)-(4x-6)≤0,则g(x)≤4x-6当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的分界直线y=4x-6.
点评:本题考查的知识点是函数的求导,利用导数求最值,属于中档题,注意做题要仔细.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
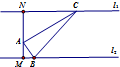 如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,
如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,