题目内容
若实数x,y满足xy=1,则x2+2y2的最小值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:由已知可得y=
,代入要求的式子,由基本不等式可得.
| 1 |
| x |
解答:
解:∵xy=1,
∴y=
∴x2+2y2=x2+
≥2
=2
,
当且仅当x2=
,即x=±
时取等号,
故答案为:2
∴y=
| 1 |
| x |
∴x2+2y2=x2+
| 2 |
| x2 |
x2•
|
| 2 |
当且仅当x2=
| 2 |
| x2 |
| 4 | 2 |
故答案为:2
| 2 |
点评:本题考查基本不等式,属基础题.

练习册系列答案
相关题目
如图程序运行后,输出的值是( )


| A、9 | B、-4 | C、14 | D、5 |
若函数f(x)为偶函数,x>0时,f(x)单调递增,P=f(-π),Q=f(e),R=f(
),则P,Q,R的大小为( )
| 2 |
| A、R>Q>P |
| B、P>Q>R |
| C、P>R>Q |
| D、Q>R>P |
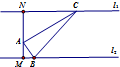 如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,
如图,A是两条平行直线l1,l2之间的一个定点,且A到l1,l2的距离分别为AM=1,AN=2,设△ABC的另两个顶点B,C分别在l1,l2上运动,且AB<AC,