题目内容

将边长为2的正方形ABCD沿对角线BD折成直二面角A-BD-C，若点A，B，C，D都在一个以O为球心的球面上，则球O的体积为
 
．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：因为外接球的球心到4顶点的距离相等，可知其球心位置和球的半径，即可求出球的体积
解答： 解：如图，折叠后的图形为三棱锥A-BCD，且平面ABD⊥平面BCD，
取BD的中点E，连接AE，CE，
∵AB=AD=2，
∴AE⊥BD．
同理，CE⊥BD，
∴∠AEC=90°，
∴EA=EB=EC=ED=
2
，
即E为外接球球心O，R=
2

∴球O的体积V=
4
3
πR3=
8
2
3
，
故答案为：
8
2
3
点评：本题考查学生对球的性质的使用和对公式的利用，其中根据已知求出球的半径是解答的关键．
练习册系列答案
相关题目
如果b是a和c的等差中项，y是x和z的等比中项，且x，y，z都是正数．则（b-c）logmx+（c-a） logmy+（a-b） logmz=
 
，其中m＞0且m≠1．
已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积为
 
．
若集合A={x|ln（x-1）＜1}，B={x|
1
4
＜（
1
2
）x＜1}，则集合A∩B=
 
．
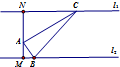如图，A是两条平行直线l1，l2之间的一个定点，且A到l1，l2的距离分别为AM=1，AN=2，设△ABC的另两个顶点B，C分别在l1，l2上运动，且AB＜AC，
AB
cos∠ABC
=
AC
cos∠ACB
，则以下结论正确的序号是
 
．
①△ABC是直角三角形；
②
1
AB
+
2
AC
的最大值为
2
；
③（S四边形MBCN）min=（S△ABC）min+（S△AMB+S△ACN）min；
④设△AMB的周长为y1，△ACN的周长为y2，则（y1+y2）min=10．
定义：关于x的不等式|x-A|＜B的解集叫A的B邻域．已知a+b-2的a+b邻域为区间（-2，8），其中a、b分别为椭圆
x2
a2
+
y2
b2
=1的长半轴和短半轴．若此椭圆的一焦点与抛物线y2=4
5
x的焦点重合，则椭圆的方程为
 
．
在平面直角坐标系xOy中，过定点Q（1，1）的直线l与曲线C：y=
x
x-1
交于M，N点，则
ON
•
OQ
-
MQ
•
OQ
=
 
．
已知互异的复数a，b满足ab≠0，集合{a，b}={a2，b2}，则a+b=
 
．
由函数y=cosx与x=0，x=
5
6
π，y=0围成的几何图形的面积为（　　）
A、
1
4
B、
1
2
C、
3
4
D、
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网