题目内容
|x2+x+2|x+4|+1|≤x2的解集为 ．
考点：绝对值不等式的解法
专题：计算题,不等式
分析：利用绝对值的几何意义，去掉绝对值，再解不等式，即可得出结论．
解答：
解：|x2+x+2|x+4|+1|≤x2可化为-x2≤x2+x+2|x+4|+1≤x2，
∴2x2+x+2|x+4|+1≥0且x+2|x+4|+1≤0，
∴x+4≥0时，2x2+3x+9≥0且3x+9≤0，解得x≤-3，∴-4≤x≤-3；
x+4＜0时，2x2-x-7≥0且-x-7≤0，解得-7≤x＜-4；
综上，-7≤x≤-3．
故答案为：{x|-7≤x≤-3}．
∴2x2+x+2|x+4|+1≥0且x+2|x+4|+1≤0，
∴x+4≥0时，2x2+3x+9≥0且3x+9≤0，解得x≤-3，∴-4≤x≤-3；
x+4＜0时，2x2-x-7≥0且-x-7≤0，解得-7≤x＜-4；
综上，-7≤x≤-3．
故答案为：{x|-7≤x≤-3}．
点评：本题考查绝对值不等式的解法，考查学生的计算能力，正确利用绝对值的几何意义，去掉绝对值是关键．
练习册系列答案
相关题目
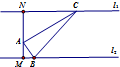如图，A是两条平行直线l1，l2之间的一个定点，且A到l1，l2的距离分别为AM=1，AN=2，设△ABC的另两个顶点B，C分别在l1，l2上运动，且AB＜AC，若（x+2i）•i=y-2i，x，y∈R，则复数x+yi=（ ）
| A、-2-2i | B、1+2i |
| C、2+i | D、2+2i |