题目内容
已知函数f(x)=(a2+8)ex,函数g(x)=(x2+ax-2a-3)e3-x.
(1)若a=0,求g(x)的单调递增区间;
(2)若a>0,且存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|min<3,求实数a的取值范围.
(1)若a=0,求g(x)的单调递增区间;
(2)若a>0,且存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|min<3,求实数a的取值范围.
考点:利用导数求闭区间上函数的最值,函数的单调性及单调区间,函数的最值及其几何意义
专题:导数的综合应用
分析:(1)先求导函数,利用导数和单调性的关系即可求出函数单调增区间;
(2)分别求出fmin(x)与gmax(x),再将问题等价转化为:若存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<3,只要fmin(x)-gmax(x)<3即可,从而解不等式,即可求出a的取值范围.
(2)分别求出fmin(x)与gmax(x),再将问题等价转化为:若存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<3,只要fmin(x)-gmax(x)<3即可,从而解不等式,即可求出a的取值范围.
解答:
解:(1)若a=0,则g(x)=(x2-3)e3-x.
则g'(x)=2xe3-x-(x2-3)e3-x=(-x2+2x+3)e3-x.
由g'(x)=(-x2+2x+3)e3-x≥0,
得-x2+2x+3≥0,解得-1≤x≤3,
即g(x)的单调递增区间为[-1,3];
(2)g'(x)=-[x2+(a-2)x-3a-3]e3-x=-(x-3)(x+a+1)e3-x
∵a>0,∴-(a+1)<0
∴当x∈[0,3]时g(x)单调递增,
当x∈[3,4]时,g(x)单调递减,
∴当x∈[0,4]时,gmax(x)=g(3)=a+6,
∵f(x)=(a2+8)ex在x∈[0,4]时是增函数,fmin(x)=f(0)=a2+8,
又∵a2+8-(a+6)=a2-a+2=(a-
) 2+
>0,
∴fmin(x)>gmax(x),
∴当x∈[0,4]时,f(x)>g(x)恒成立.
∴若存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<3
只要fmin(x)-gmax(x)<3即可,
即a2+8-(a+6)<3,
∴a2-a-1<0,
解
<a<
,
∵a>0,
∴0<a<
,
即a的取值范围为:0<a<
.
则g'(x)=2xe3-x-(x2-3)e3-x=(-x2+2x+3)e3-x.
由g'(x)=(-x2+2x+3)e3-x≥0,
得-x2+2x+3≥0,解得-1≤x≤3,
即g(x)的单调递增区间为[-1,3];
(2)g'(x)=-[x2+(a-2)x-3a-3]e3-x=-(x-3)(x+a+1)e3-x
∵a>0,∴-(a+1)<0
∴当x∈[0,3]时g(x)单调递增,
当x∈[3,4]时,g(x)单调递减,
∴当x∈[0,4]时,gmax(x)=g(3)=a+6,
∵f(x)=(a2+8)ex在x∈[0,4]时是增函数,fmin(x)=f(0)=a2+8,
又∵a2+8-(a+6)=a2-a+2=(a-
| 1 |
| 2 |
| 7 |
| 4 |
∴fmin(x)>gmax(x),
∴当x∈[0,4]时,f(x)>g(x)恒成立.
∴若存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<3
只要fmin(x)-gmax(x)<3即可,
即a2+8-(a+6)<3,
∴a2-a-1<0,
解
1-
| ||
| 2 |
1+
| ||
| 2 |
∵a>0,
∴0<a<
1+
| ||
| 2 |
即a的取值范围为:0<a<
1+
| ||
| 2 |
点评:本题主要考查了利用导数求闭区间上函数的最值,以及利用导数研究函数的单调性,同时考查了分类讨论的数学思想,综合性较强,运算量较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a=log54,b=(log53)2,c=log45,则a,b,c的大小关系为( )
| A、a<c<b |
| B、b<a<c |
| C、a<b<c |
| D、b<c<a |
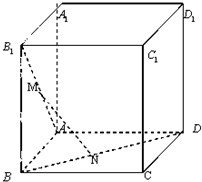 如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<
如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<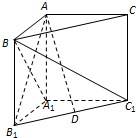 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.