题目内容
设抛物线y2=4x上的一点P到y轴的距离是4,则点P到该抛物线焦点的距离为( )
| A、3 | B、4 | C、5 | D、6 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意可得点P的横坐标为4,由抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线x=-1的距离,由此求得结果.
解答:
解:由于抛物线y2=4x上一点P到y轴的距离是4,故点P的横坐标为4.
再由抛物线y2=4x的准线为x=-1,
以及抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线的距离,
故点P到该抛物线焦点的距离是4-(-1)=5,
故选:C.
再由抛物线y2=4x的准线为x=-1,
以及抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线的距离,
故点P到该抛物线焦点的距离是4-(-1)=5,
故选:C.
点评:本题主要考查抛物线的定义、标准方程,以及简单性质的应用,属于基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
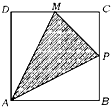 如图,点P在边长为1的正方形的边上运动,设M是CD的中点,则当P沿着路径A-B-C-M运动时,点P经过的路程x与△APM的面积y的函数关系为y=f(x),则y=f(x)的图象是
如图,点P在边长为1的正方形的边上运动,设M是CD的中点,则当P沿着路径A-B-C-M运动时,点P经过的路程x与△APM的面积y的函数关系为y=f(x),则y=f(x)的图象是( )
A、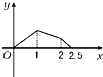 |
B、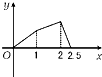 |
C、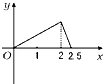 |
D、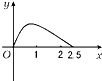 |
下列函数中,在其定义域内既是奇函数,又是减函数的是( )
| A、y=-x3 | ||
| B、y=sinx | ||
| C、y=tanx | ||
D、y=(
|
不等式的(x-2)(2x-3)<0解集是( )
A、(-∞,
| ||
| B、R | ||
C、(
| ||
| D、φ |
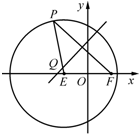 如图,已知圆E:
如图,已知圆E: