题目内容
已知点A,B,C,D的坐标分别为A(1,0),B(0,1),C(cosα,sinα),α∈[0,2π).
(1)若|
|=|
|,求角α的值;
(2)若
•
=
,求
的值.
(1)若|
| AC |
| BC |
(2)若
| AC |
| AC |
| 1 |
| 3 |
| 2sin2α+2sinαcosα |
| 1+tanα |
考点:三角函数的化简求值,向量的模,平面向量数量积的运算
专题:三角函数的求值
分析:(1)利用向量的数量积及向量模的运算性质可求得tanα=1,α∈[0,2π),从而可得答案;
(2)由
•
=
⇒sinα+cosα=
,等号两边平方可得2sinαcosα=-
,将所求关系式中的弦化切即可求得答案.
(2)由
| AC |
| BC |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
解答:
解:(1)
=(cosα-1,sinα),
=(cosα,sinα-1),
由|
|=|
|,
得
=
,
即
=
,
∴cosα=sinα,
∴tanα=1,
又α∈[0,2π),α=
或
;
(2)由
•
=
,
得(cosα-1)cosα+(sinα-1)sinα=
,
∴sinα+cosα=
.
上式两边平方得1+2sinα+cosα=
,
∴2sinαcosα=-
.
∴
=
=2sinαcosα=-
.
| AC |
| BC |
由|
| AC |
| BC |
得
| (cosα-1)2+sin2α |
| cos2α+(sinα-1)2 |
即
| 2-2cosα |
| 2-2sinα |
∴cosα=sinα,
∴tanα=1,
又α∈[0,2π),α=
| π |
| 4 |
| 5π |
| 4 |
(2)由
| AC |
| BC |
| 1 |
| 3 |
得(cosα-1)cosα+(sinα-1)sinα=
| 1 |
| 3 |
∴sinα+cosα=
| 2 |
| 3 |
上式两边平方得1+2sinα+cosα=
| 4 |
| 9 |
∴2sinαcosα=-
| 5 |
| 9 |
∴
| 2sin2α+2sinαcosα |
| 1+tanα |
| 2sinα(sinα+cosα) | ||
1+
|
| 5 |
| 9 |
点评:本题考查三角函数的化简求值,考查平面向量数量积的运算,属于中档题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
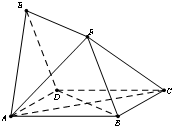 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.