题目内容
已知函数f(x)=x2-8lnx,g(x)=-x2+14x.
(1)若函数f(x)与g(x)在区间(a,a+1)上均为增函数,求a的取值范围;
(2)若方程f(x)=g(x)+m有两个不同的实数解,求实数m的取值范围.
(1)若函数f(x)与g(x)在区间(a,a+1)上均为增函数,求a的取值范围;
(2)若方程f(x)=g(x)+m有两个不同的实数解,求实数m的取值范围.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(1)分别求出两个函数的递增区间,取交集即可,(2)将问题转化为求h(x)=
x2-
x-
,m(x)=lnx的交点问题,只需h(x)min≤h(
)即可,从而求出m的值.
| 1 |
| 4 |
| 7 |
| 4 |
| m |
| 8 |
| 7 |
| 2 |
解答:
解:(1)∵f′(x)=
,令f′(x)>0,解得:x>2,
g′(x)=-2x+14,令g′(x)>0,解得:x<7,
∴2<x<7,
若函数f(x)与g(x)在区间(a,a+1)上均为增函数,
∴
,解得:2≤a≤6,
∴a的范围是[2,6].
(2)∵f(x)=g(x)+m,
∴
x2-
x-
=lnx,
令h(x)=
x2-
x-
,m(x)=lnx,
画出函数的图象,如图示:
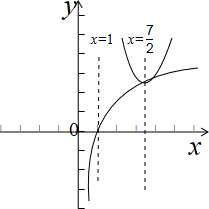 ,
,
当x=
时,m(x)=ln
,
∴只需h(x)min=-
-
<ln
即可,
∴m>-
-8ln
.
| 2(x2-4) |
| x |
g′(x)=-2x+14,令g′(x)>0,解得:x<7,
∴2<x<7,
若函数f(x)与g(x)在区间(a,a+1)上均为增函数,
∴
|
∴a的范围是[2,6].
(2)∵f(x)=g(x)+m,
∴
| 1 |
| 4 |
| 7 |
| 4 |
| m |
| 8 |
令h(x)=
| 1 |
| 4 |
| 7 |
| 4 |
| m |
| 8 |
画出函数的图象,如图示:
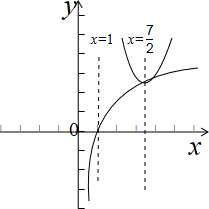 ,
,当x=
| 7 |
| 2 |
| 7 |
| 2 |
∴只需h(x)min=-
| m |
| 8 |
| 49 |
| 16 |
| 7 |
| 2 |
∴m>-
| 49 |
| 2 |
| 7 |
| 2 |
点评:本题考查了函数的单调性,导数的应用,考查数形结合,分类讨论,本题属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.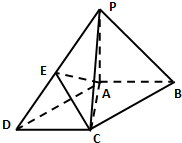 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.