题目内容
(1)化简:(0.027) -
-(-
)-2+(2
)
-(
-1)0
(2)判断圆C1:(x+1)2+(y-3)2=36与圆C2:x2+y2-4x+2y-4=0的位置关系.
| 1 |
| 3 |
| 1 |
| 7 |
| 7 |
| 9 |
| 1 |
| 2 |
| 2 |
(2)判断圆C1:(x+1)2+(y-3)2=36与圆C2:x2+y2-4x+2y-4=0的位置关系.
考点:直线与圆的位置关系,有理数指数幂的化简求值
专题:直线与圆
分析:(1)由条件利用分数指数幂的运算法则求得所给式子的值.
(2)先求出两个圆的圆心和半径以及两圆的圆心距,再根据两圆的圆心距大于半径之差而小于半径之和,可得圆C1与C2相交.
(2)先求出两个圆的圆心和半径以及两圆的圆心距,再根据两圆的圆心距大于半径之差而小于半径之和,可得圆C1与C2相交.
解答:
解:(1)(0.027)-
-(-
)-2+(2
)
-(
-1)0=(
)
-72+(
)
-1=
-49+
-1=-45.
(2)圆C1:(x+1)2+(y-3)2=36的圆心在C1(-1,3),半径r1=6.
圆C2:x2+y2-4x+2y-4=0的方程可以化作:(x-2)2+(y+1)2=9,圆心在C2(2,-1),半径r2=3.
∴|C1C2|=
=5.
又r1-r2=3,r1+r2=9,∴r1-r2<|C1C2|<r1+r2,∴圆C1与C2相交.
| 1 |
| 3 |
| 1 |
| 7 |
| 7 |
| 9 |
| 1 |
| 2 |
| 2 |
| 1000 |
| 27 |
| 1 |
| 3 |
| 25 |
| 9 |
| 1 |
| 2 |
| 10 |
| 3 |
| 5 |
| 3 |
(2)圆C1:(x+1)2+(y-3)2=36的圆心在C1(-1,3),半径r1=6.
圆C2:x2+y2-4x+2y-4=0的方程可以化作:(x-2)2+(y+1)2=9,圆心在C2(2,-1),半径r2=3.
∴|C1C2|=
| (2+1)2+(-1-3)2 |
又r1-r2=3,r1+r2=9,∴r1-r2<|C1C2|<r1+r2,∴圆C1与C2相交.
点评:本题主要考查分数指数幂的运算法则的应用,圆的标准方程,两个圆的位置关系的判定方法,属于基础题.

练习册系列答案
相关题目
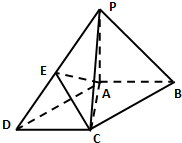 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点. 如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2
如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2