题目内容
11.不存在函数f(x)满足,对任意x∈R都有( )| A. | f(|x+1|)=x2+2x | B. | f(cos2x)=cosx | C. | f(sinx)=cos2x | D. | f(cosx)=cos2x |
分析 若f(cos2x)=cosx,则有f(1)=1且f(1)=-1,根据函数的定义,可得结论.
解答 解:若f(|x+1|)=x2+2x=(x+1)2-1,
则f(x)=x2-1,x≥1,故存在函数f(x),使A成立;
若f(sinx)=cos2x=1-2sin2x,
则f(x)=1-2x2,-1≤x≤1,故存在函数f(x),使C成立;
若f(cosx)=cos2x=2cos2x-1,
则f(x)=2x2-1,-1≤x≤1,故存在函数f(x),使D 成立;
当x=0时,f(cos2x)=cosx可化为:f(1)=1,
当x=π时,f(cos2x)=cosx可化为:f(1)=-1,
这与函数定义域,每一个自变量都有唯一的函数值与其对应矛盾,
故不存在函数f(x)对任意x∈R都有f(cos2x)=cosx,
故选:B.
点评 本题考查的知识点是抽象函数及其应用,函数的定义,难度中档.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
19.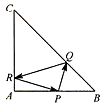 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
6.若角θ是第四象限的角,则角${-^{\;}}\frac{θ}{2}$是( )
| A. | 第一、三象限角 | B. | 第二、四象限角 | C. | 第二、三象限角 | D. | 第一、四象限角 |
3.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为$\frac{7}{8}$.
20.下列说法中正确的是( )
| A. | 经过不同的三点有且只有一个平面 | |
| B. | 没有公共点的两条直线一定平行 | |
| C. | 垂直于同一平面的两直线是平行直线 | |
| D. | 垂直于同一平面的两平面是平行平面 |