题目内容
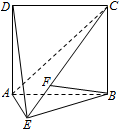 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥平面BCE;
(2)求BF与平面ABCD所成的角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得BF⊥AE,从而平面ABCD⊥平面ABE,由BC⊥AB,得BC⊥平面ABE,从而BC⊥AE,由此能证明AE⊥平面BCE.
(2)取AB的中点O,连结OC、OE,过F作FG∥OE,交OC于G,由已知得∠FBG为BF与平面ABCD所成的角,由此能求出BF与平面ABCD所成的角的正弦值.
(2)取AB的中点O,连结OC、OE,过F作FG∥OE,交OC于G,由已知得∠FBG为BF与平面ABCD所成的角,由此能求出BF与平面ABCD所成的角的正弦值.
解答:
(1)证明:∵BF⊥平面ACE,
∴BF⊥AE,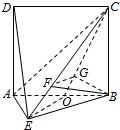
∵二面角D-AB-E为直二面角,
∴平面ABCD⊥平面ABE,
又BC⊥AB,
∴BC⊥平面ABE,
∴BC⊥AE,
又BF?平面BCE,BC?平面BCE,BF∩BC=B,
∴AE⊥平面BCE.
(2)解:取AB的中点O,连结OC、OE,过F作FG∥OE,交OC于G,
∵二面角D-AB-E为直二面角,∴平面ABCD⊥平面ABE,
∴OE⊥平面ABCD,∴FG⊥平面ABCD,
∴∠FBG为BF与平面ABCD所成的角,
由(1)知,AE⊥平面BCE,∴AE⊥EB,
又AE=EB,AB=2,AE=BE=
,EO=1,
在直角三角形BCE中,CE=
=
,
BF=
=
=
,FC=
,
∴FG=
OE=
,
在直角三角形BGF中,sin∠FBG=
=
=
,
∴BF与平面ABCD所成的角的正弦值为
.
∴BF⊥AE,

∵二面角D-AB-E为直二面角,
∴平面ABCD⊥平面ABE,
又BC⊥AB,
∴BC⊥平面ABE,
∴BC⊥AE,
又BF?平面BCE,BC?平面BCE,BF∩BC=B,
∴AE⊥平面BCE.
(2)解:取AB的中点O,连结OC、OE,过F作FG∥OE,交OC于G,
∵二面角D-AB-E为直二面角,∴平面ABCD⊥平面ABE,
∴OE⊥平面ABCD,∴FG⊥平面ABCD,
∴∠FBG为BF与平面ABCD所成的角,
由(1)知,AE⊥平面BCE,∴AE⊥EB,
又AE=EB,AB=2,AE=BE=
| 2 |
在直角三角形BCE中,CE=
| BC2+BE2 |
| 6 |
BF=
| BC•BE |
| CE |
2
| ||
| 6 |
| 2 | ||
|
2
| ||
| 3 |
∴FG=
| 2 |
| 3 |
| 2 |
| 3 |
在直角三角形BGF中,sin∠FBG=
| FG |
| BF |
| ||||
|
| ||
| 3 |
∴BF与平面ABCD所成的角的正弦值为
| ||
| 3 |
点评:本题考查直线与平面垂直的判定定理、平面与平面垂直的性质定理、勾股定理、二面角的求解等基础知识和空间向量的立体几何中的应用,意在考查方程思想、等价转化思想等数学思想方法和考生的空间想象能力、逻辑推理能力和运算求解能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
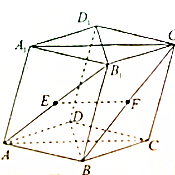 如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )
如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
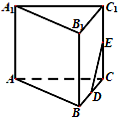 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=