题目内容
已知函数f(x)=
和直线l:y=m(x-1).
(1)当曲线y=f(x)在点(1,f(1))处的切线与直线l垂直时,求原点O到直线l的距离;
(2)若对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立,求m的取值范围;
(3)求证:ln
<
(n∈N+)
| xlnx |
| x+1 |
(1)当曲线y=f(x)在点(1,f(1))处的切线与直线l垂直时,求原点O到直线l的距离;
(2)若对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立,求m的取值范围;
(3)求证:ln
| 4 | 2n+1 |
| n |
 |
| i=1 |
| i |
| 4i2-1 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数,得到f(1)=
,由曲线y=f(x)在点(1,f(1))处的切线与直线l垂直求出m=-2,则直线l的方程可求,由点到直线的距离公式得答案;
(Ⅱ)把对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立转化为lnx≤m(x-
),然后构造函数g(x)=lnx-m(x-
),利用导数对m≤0和m>0分类讨论求得m的取值范围;
(Ⅲ)由(Ⅱ)知,当x>1,m=
时,lnx<
(x-
)成立,令x=
,(k∈N*),结合不等式
<
(
-
)=
得到不等式
[ln(2k+1)-ln(2k-1)]<
,(k∈N*),即
(ln3-ln1)<
,然后利用累加求和得答案.
| 1 |
| 2 |
(Ⅱ)把对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立转化为lnx≤m(x-
| 1 |
| x |
| 1 |
| x |
(Ⅲ)由(Ⅱ)知,当x>1,m=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 2k+1 |
| 2k-1 |
| 2k+1 |
| 2k-1 |
| 1 |
| 2 |
| 2k+1 |
| 2k-1 |
| 2k-1 |
| 2k+1 |
| 4k |
| 4k2-1 |
| 1 |
| 4 |
| 4k |
| 4k2-1 |
| 1 |
| 4 |
| 1 |
| 4×12-1 |
解答:
(Ⅰ)解:由f(x)=
,得f′(x)=
,
∴f(1)=
,于是m=-2,直线l的方程为2x+y-2=0.
原点O到直线l的距离为
=
;
(Ⅱ)解:对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立,即
≤m(x-1),也就是lnx≤m(x-
),
设g(x)=lnx-m(x-
),即?x∈[1,+∞),g(x)≤0成立.
g′(x)=
-m(1+
)=
.
①若m≤0,?x使g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾;
②若m>0,方程-mx2+x-m=0的判别式△=1-4m2,
当△≤0,即m≥
时,g′(x)≤0,
∴g(x)在(1,+∞)上单调递减,
∴g(x)≤g(1)=0,即不等式成立.
当0<m<
时,方程-mx2+x-m=0的两根为x1,x2(x1<x2),
x1=
∈(0,1),x2=
∈(1,+∞),
当x∈(x1,x2)时,g′(x)>0,g(x)单调递增,g(x)>g(1)=0与题设矛盾.
综上所述,m≥
;
(Ⅲ)证明:由(Ⅱ)知,当x>1,m=
时,lnx<
(x-
)成立.
不妨令x=
,(k∈N*),
∴
<
(
-
)=
,
[ln(2k+1)-ln(2k-1)]<
,(k∈N*).
∴
(ln3-ln1)<
.
(ln5-ln3)<
.
…
(ln(2n+1)-ln(2n-1))<
.
累加可得:
ln(2n+1)<
,(n∈N*).
即ln
<
(n∈N*).
| xlnx |
| x+1 |
| x+1+lnx |
| (x+1)2 |
∴f(1)=
| 1 |
| 2 |
原点O到直线l的距离为
| |-2| | ||
|
2
| ||
| 5 |
(Ⅱ)解:对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立,即
| xlnx |
| x+1 |
| 1 |
| x |
设g(x)=lnx-m(x-
| 1 |
| x |
g′(x)=
| 1 |
| x |
| 1 |
| x2 |
| -mx2+x-m |
| x2 |
①若m≤0,?x使g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾;
②若m>0,方程-mx2+x-m=0的判别式△=1-4m2,
当△≤0,即m≥
| 1 |
| 2 |
∴g(x)在(1,+∞)上单调递减,
∴g(x)≤g(1)=0,即不等式成立.
当0<m<
| 1 |
| 2 |
x1=
1-
| ||
| 2m |
1+
| ||
| 2m |
当x∈(x1,x2)时,g′(x)>0,g(x)单调递增,g(x)>g(1)=0与题设矛盾.
综上所述,m≥
| 1 |
| 2 |
(Ⅲ)证明:由(Ⅱ)知,当x>1,m=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
不妨令x=
| 2k+1 |
| 2k-1 |
∴
| 2k+1 |
| 2k-1 |
| 1 |
| 2 |
| 2k+1 |
| 2k-1 |
| 2k-1 |
| 2k+1 |
| 4k |
| 4k2-1 |
| 1 |
| 4 |
| 4k |
| 4k2-1 |
∴
| 1 |
| 4 |
| 1 |
| 4×12-1 |
| 1 |
| 4 |
| 2 |
| 4×22-1 |
…
| 1 |
| 4 |
| n |
| 4n2-1 |
累加可得:
| 1 |
| 4 |
| n |
 |
| i=1 |
| i |
| 4i2-1 |
即ln
| 4 | 2n+1 |
| ||
| n+1 |
| i |
| 4i2-1 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了利用导数证明函数表达式,对于(Ⅲ)的证明,引入不等式
<
(
-
)=
是关键,要求考生具有较强的逻辑思维能力和灵活变形能力,是压轴题.
| 2k+1 |
| 2k-1 |
| 1 |
| 2 |
| 2k+1 |
| 2k-1 |
| 2k-1 |
| 2k+1 |
| 4k |
| 4k2-1 |

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2011年3月发生在日本的9级大地震虽然过去多年了,但它对日本的核电站的破坏却是持续的,其中有一种放射性元素铯137在其衰变过程中,假设近似满足:其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M02-
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10ln2(太贝克/年),则M(60)等于( )
| t |
| 30 |
| A、5太贝克 |
| B、72ln 2太贝克 |
| C、150ln 2太贝克 |
| D、150太贝克 |
设P为锐角△ABC的外心(三角形外接圆圆心),
=k(
+
)(k∈R).若cos∠BAC=
,则k=( )
| AP |
| AB |
| AC |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列几何体中不是旋转体的是( )
A、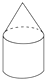 |
B、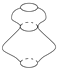 |
C、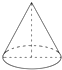 |
D、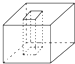 |
如果圆柱与圆锥的底面直径、高和球的直径相等,则体积比V圆柱:V圆锥:V球为( )
| A、3:1:2 | ||
| B、3:1:4 | ||
C、6:
| ||
| D、3:3:2 |
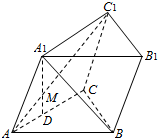 如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.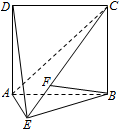 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.