题目内容
一个圆锥的侧面展开图是圆心角为
π;则圆锥母线与底面所成角的余弦值为 .
| 4 |
| 3 |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:设母线长为l,底面半径为r,利用侧面展开图,求出圆心角,然后求出底面半径,即可求出圆锥母线与底面所成角的余弦值.
解答:
解:设母线长为l,底面半径为r,
由θ=
=
π,
∴r=
l,
因此所求角的余弦值即为
=
.
故答案为:
.
由θ=
| 2πr |
| l |
| 4 |
| 3 |
∴r=
| 2 |
| 3 |
因此所求角的余弦值即为
| r |
| l |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题是基础题,考查圆锥的侧面展开图,扇形的知识,圆锥的母线与底面所成的角,考查计算能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
设P为锐角△ABC的外心(三角形外接圆圆心),
=k(
+
)(k∈R).若cos∠BAC=
,则k=( )
| AP |
| AB |
| AC |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中正确的是( )
| A、有两个面互相平行,其余各面都是平行四边形的几何体是棱柱 |
| B、用一个平面去截一个圆锥,只能得到一个圆锥和一个圆台 |
| C、有一个面是多边形,其余面都是三角形的几何体是棱锥 |
| D、将一个直角三角形绕其一条直角边旋转一周,所得圆锥母线长等于斜边长 |
下列几何体中不是旋转体的是( )
A、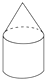 |
B、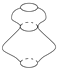 |
C、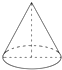 |
D、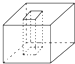 |
已知MP、OM、AT分别是60°角的正弦线、余弦线、正切线,如图,则一定有( )
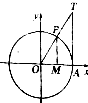

| A、MP<OM<AT |
| B、AT<OM<MP |
| C、OM<MP<AT |
| D、OM<AT<MP |
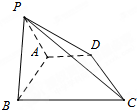 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=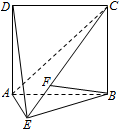 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.