题目内容
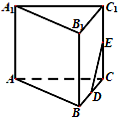 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=| 2 |
(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(2)设点M为线段AB的中点,证明:直线DE∥平面A1MC;
(3)在(1)条件下,求点D到平面A1B1E1的距离.
考点:直线与平面垂直的判定,直线与平面平行的判定,点、线、面间的距离计算
专题:证明题,空间位置关系与距离
分析:(1)先证明AA1⊥平面ABC,可得AA1⊥BC,利用AC⊥BC,可以证明直线BC⊥平面ACC1A1.
(2)取AB的中点M,连接A1M,MC,A1C,AC1,证明四边形MDEO为平行四边形即可.
(3)由(1)可证A1C1⊥平面BCC1B1,由题意可得
VD-A1B1E=
S△B1DE•A1C1,又可求A1E,B1E,从而求得S△A1B1E,S△B1DE,由体积公式即可求得
点D到平面A1B1E的距离.
(2)取AB的中点M,连接A1M,MC,A1C,AC1,证明四边形MDEO为平行四边形即可.
(3)由(1)可证A1C1⊥平面BCC1B1,由题意可得
| 1 |
| 3 |
| 1 |
| 3 |
点D到平面A1B1E的距离.
解答:
 (本小题满分14分)
(本小题满分14分)
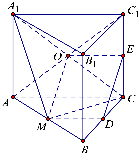
解:(1)因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.…(1分)
因为AB,AC为平面ABC内的两条相交直线,
所以AA1⊥平面ABC.因为直线BC?平面ABC内,所以AA1⊥BC.…(3分)
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内的两条相交直线,
所以,BC⊥平面ACC1A1.…(5分)
(2)因为点M为线段AB的中点,连接A1M,MC,A1C,AC1,连接OM,
设O为A1C,AC1的交点.由已知,O为AC1的中点.…(6分)
连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线.
所以,MD∥AC,OE∥AC且MD=
AC,OE=
AC,…(7分)
所以MD∥OE且MD=OE …(8分)
从而四边形MDEO为平行四边形,则DE∥MO.
因为直线DE?平面A1MC,MO?平面A1MC,所以直线DE∥平面A1MC …(9分)
(3)由(1)BC⊥平面ACC1A1,所以BC⊥A1C1,
又CC1⊥A1C1,CC1∩BC=C所以A1C1⊥平面BCC1B1,…(10分)
由题意VD-A1B1E=VA1-B1DE,所以
VD-A1B1E=
S△B1DE•A1C1,…(11分)
A1E=B1E=
=
,所以S△A1B1E=
×2×
=
,…(12分)
S△B1DE=SBCC1B1-S△B1C1E-S△EB1D-S△DCE=
-
-
-
=
,…(13分)
所以
•
•h=
•
•
,
所以h=
,点D到平面A1B1E的距离为
.…(14分)
 (本小题满分14分)
(本小题满分14分)解:(1)因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.…(1分)
因为AB,AC为平面ABC内的两条相交直线,
所以AA1⊥平面ABC.因为直线BC?平面ABC内,所以AA1⊥BC.…(3分)
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内的两条相交直线,
所以,BC⊥平面ACC1A1.…(5分)
(2)因为点M为线段AB的中点,连接A1M,MC,A1C,AC1,连接OM,
设O为A1C,AC1的交点.由已知,O为AC1的中点.…(6分)
连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线.
所以,MD∥AC,OE∥AC且MD=
| 1 |
| 2 |
| 1 |
| 2 |
所以MD∥OE且MD=OE …(8分)
从而四边形MDEO为平行四边形,则DE∥MO.
因为直线DE?平面A1MC,MO?平面A1MC,所以直线DE∥平面A1MC …(9分)
(3)由(1)BC⊥平面ACC1A1,所以BC⊥A1C1,
又CC1⊥A1C1,CC1∩BC=C所以A1C1⊥平面BCC1B1,…(10分)
由题意VD-A1B1E=VA1-B1DE,所以
| 1 |
| 3 |
| 1 |
| 3 |
A1E=B1E=
(
|
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
S△B1DE=SBCC1B1-S△B1C1E-S△EB1D-S△DCE=
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 8 |
3
| ||
| 8 |
所以
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
3
| ||
| 8 |
| 2 |
所以h=
3
| ||
| 10 |
3
| ||
| 10 |
点评:本题考查线面垂直的判定与性质的运用,考查存在性问题,考查学生分析解决问题的能力,考查了转化思想,属于中档题.

练习册系列答案
相关题目
2011年3月发生在日本的9级大地震虽然过去多年了,但它对日本的核电站的破坏却是持续的,其中有一种放射性元素铯137在其衰变过程中,假设近似满足:其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M02-
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10ln2(太贝克/年),则M(60)等于( )
| t |
| 30 |
| A、5太贝克 |
| B、72ln 2太贝克 |
| C、150ln 2太贝克 |
| D、150太贝克 |
设P为锐角△ABC的外心(三角形外接圆圆心),
=k(
+
)(k∈R).若cos∠BAC=
,则k=( )
| AP |
| AB |
| AC |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“
=0”是“(x1,y1)、(x2,y2)、(x3,y3)三点共线”的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
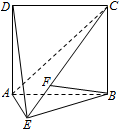 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.