题目内容
19.如果两非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,那么$\overrightarrow{a}$与$\overrightarrow{b}$反向,则( )| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|-|$\overrightarrow{a}$| | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
分析 由已知可得$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$||$\overrightarrow{b}$|,进而可得|$\overrightarrow{a}$+$\overrightarrow{b}$|2=(|$\overrightarrow{a}$|-|$\overrightarrow{b}$|)2,进而得到答案.
解答 解:∵|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,那么$\overrightarrow{a}$与$\overrightarrow{b}$反向,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$||$\overrightarrow{b}$|,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$+$\overrightarrow{b}$)2=$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|+|$\overrightarrow{b}$|2=(|$\overrightarrow{a}$|-|$\overrightarrow{b}$|)2,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,
故选:A
点评 本题考查的知识点是向量的模,向量的数量积,难度中档.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
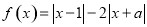 .
.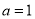 时,求不等式
时,求不等式 的解集;
的解集;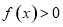 ,在
,在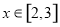 上恒成立,求
上恒成立,求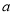 的取值范围.
的取值范围.