题目内容
4．曲线y=（x-2）e2x在点A（0，-2）处的切线方程．分析 求出导函数，求出切线斜率，利用点斜式可得切线方程．
解答 解：由于y=（x-2）e2x，可得y′=（2x-3）e2x，
令x=0，可得y′=-3，
∴曲线y=（x-2）e2x在点A（0，-2）处的切线方程为y+2=-3x，
即y=-3x-2．
点评 本题考查导数的几何意义，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
19．如果两非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足：|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，那么$\overrightarrow{a}$与$\overrightarrow{b}$反向，则（ ）
| A． | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | B． | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C． | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|-|$\overrightarrow{a}$| | D． | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
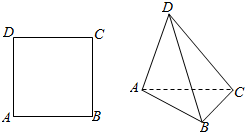把边长为2的正方形ABCD沿对角线AC折成直二面角．求：