题目内容
9.若等差数列{an}中,已知a2+a6=16,s6=39,求d,an.分析 等差数列的通项公式与前n项和,列出方程组求出a1与d,写出通项公式an即可.
解答 解:等差数列{an}中,
a2+a6=16,s6=39,
∴$\left\{\begin{array}{l}{{a}_{1}+d{+a}_{1}+5d=16}\\{{6a}_{1}+15d=39}\end{array}\right.$,
解得a1=-1,d=3;
∴通项公式an=-1+(n-1)×3=3n-4.
点评 本题考查了等差数列的通项公式与前n项和的应用问题,是基础题目.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4.设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
| A. | $\frac{{a}_{5}}{{a}_{2}}$ | B. | $\frac{{S}_{5}}{{S}_{3}}$ | C. | $\frac{{a}_{n+1}}{{a}_{n}}$ | D. | $\frac{{S}_{n+1}}{{S}_{n}}$ |
19.如果两非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,那么$\overrightarrow{a}$与$\overrightarrow{b}$反向,则( )
| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|-|$\overrightarrow{a}$| | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
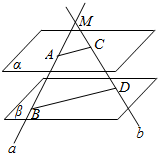 如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.
如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.