题目内容
7.若$\overrightarrow{AB}$=(4,-4,7)的终点B的坐标为(2,-1,7),则起点A的坐标为(-2,3,0).分析 若A(x1,y1,z1),B(x2,y2,z2),则$\overrightarrow{AB}$=(x2-x1,y2-y1,z2-z1).
解答 解:∵$\overrightarrow{AB}$=(4,-4,7)的终点B的坐标为(2,-1,7),
∴起点A的坐标为:
(2,-1,7)-(4,-4,7)=(-2,3,0).
故答案为:(-2,3,0).
点评 本题考查空间向量起点坐标的求法,是基础题,解题时要认真审题,注意向量坐标运算法则的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.关于x与y有如下数据:
有如下两个线性模型:
①$\stackrel{∧}{y}$=6.5x+17.5;②)$\stackrel{∧}{y}$=7x+17.试比较哪个拟合效果好.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
①$\stackrel{∧}{y}$=6.5x+17.5;②)$\stackrel{∧}{y}$=7x+17.试比较哪个拟合效果好.
19.如果两非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,那么$\overrightarrow{a}$与$\overrightarrow{b}$反向,则( )
| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|-|$\overrightarrow{a}$| | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
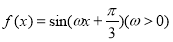 的图象的相邻两条对称轴间的距离是
的图象的相邻两条对称轴间的距离是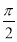 .若将函数
.若将函数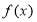 的图象向右平移
的图象向右平移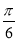 个单位,,再把图像上每个点的横坐标缩小为原来的一半,得到
个单位,,再把图像上每个点的横坐标缩小为原来的一半,得到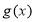 ,则
,则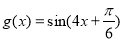 B.
B.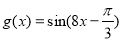
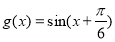 D.
D.