题目内容
9.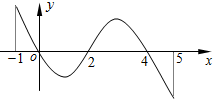 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
⑤函数y=f(x)-a的零点个数可能为0,1,2,3,4.
其中正确命题的个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 由导数图象可知,函数的单调性,从而可得函数的极值,故可得①错误,②正确;因为在当x=0和x=4,函数取得极大值f(0)=2,f(4)=2,要使当x∈[-1,t]函数f(x)的最大值是4,当2≤t≤5,所以t的最大值为5,所以③不正确;由f(x)=a知,因为极小值f(2)未知,所以无法判断函数y=f(x)-a有几个零点,所以④不正确,根据函数的单调性和极值,做出函数的图象如图,即可求得结论.
解答 解:由导数图象可知,当-1<x<0或2<x<4时,f'(x)>0,函数单调递增,
当0<x<2或4<x<5,f'(x)<0,函数单调递减,
当x=0和x=4,函数取得极大值f(0)=2,f(4)=2,当x=2时,函数取得极小值f(2),
所以①错误;②正确;
因为在当x=0和x=4,函数取得极大值f(0)=2,f(4)=2,
要使当x∈[-1,t]函数f(x)的最大值是4,
当2≤t≤5,所以t的最大值为5,所以③不正确;
由f(x)=a知,因为极小值f(2)未知,
所以无法判断函数y=f(x)-a有几个零点,所以④不正确,
根据函数的单调性和极值,做出函数的图象如图,(线段只代表单调性),
根据题意函数的极小值不确定,分f(2)<1或1≤f(2)<2两种情况,
由图象知,函数y=f(x)和y=a的交点个数有0,1,2,3,4等不同情形,所以⑤正确,
综上正确的命题序号为②⑤.
故选:B.
点评 本题考查导数知识的运用,考查导函数与原函数图象之间的关系,正确运用导函数图象是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
8.为了得到函数y=sin(3x+$\frac{π}{3}$)的图象,只需把函数y=sin3x的图象上所有的点( )
| A. | 向左平移 $\frac{π}{3}$个单位长度 | B. | 向左平移 $\frac{π}{9}$ 个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$ 个单位长度 | D. | 向右平移 $\frac{π}{9}$个单位长度 |
14.已知x,y∈R,命题p:若x>|y|,则x>y;命题q:若x+y>0,则x2>y2,在命题(1)p∨q;(2)(¬p)∧(¬q);(3)p∧(¬q);(4)p∧q中,证明题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.某学校研究性学习课题组为了研究学生的数学成绩优秀和物理成绩优秀之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:
规定:数学、物理成绩90分(含90分)以上为优秀.
(Ⅰ)根据上表完成下面的2×2列联表,并说明能否有99%的把握认为学生的数学成绩优秀与物理成绩优秀之间有关系?
(Ⅱ)记数学、物理成绩均优秀的6名学生为A、B、C、D、E、F,现从中选2名学生进行自主招生培训,求A、B两人中至少有一人被选中的概率.
参考公式及数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 92 | 72 | 93 |
| 物理 | 90 | 63 | 72 | 92 | 91 | 71 | 58 | 91 | 93 | 81 | 77 | 82 | 48 | 91 | 69 | 96 | 61 | 84 | 78 | 93 |
(Ⅰ)根据上表完成下面的2×2列联表,并说明能否有99%的把握认为学生的数学成绩优秀与物理成绩优秀之间有关系?
 | 优秀 | 不优秀 | 合计 |
| 优秀 | 6 | 2 | 8 |
| 不优秀 | 2 | 10 | 12 |
| 合计 | 8 | 12 | 20 |
参考公式及数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
18.设集合A={y|y=sinx,x∈R},B={x|y=lg(-x)},则A∩B=( )
| A. | (0,1] | B. | [-1,0) | C. | [-1,0] | D. | (-∞,1] |
19.已知数列1,4,9,16,…,则256是数列的( )
| A. | 第14项 | B. | 第15项 | C. | 第16项 | D. | 第17项 |