题目内容
1.某学校研究性学习课题组为了研究学生的数学成绩优秀和物理成绩优秀之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 92 | 72 | 93 |
| 物理 | 90 | 63 | 72 | 92 | 91 | 71 | 58 | 91 | 93 | 81 | 77 | 82 | 48 | 91 | 69 | 96 | 61 | 84 | 78 | 93 |
(Ⅰ)根据上表完成下面的2×2列联表,并说明能否有99%的把握认为学生的数学成绩优秀与物理成绩优秀之间有关系?
 | 优秀 | 不优秀 | 合计 |
| 优秀 | 6 | 2 | 8 |
| 不优秀 | 2 | 10 | 12 |
| 合计 | 8 | 12 | 20 |
参考公式及数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
分析 (Ⅰ)根据题意,列出2×2列联表,求出观测值K2,根据观测值对应的数值得出结论.
(Ⅱ)求出选2名学生进行自主招生培训的事件数,求出A、B两人中至少有一人被选中事件数,然后求解概率.
解答 解:(Ⅰ)根据题意,列出2×2列联表,如下
 | 优秀 | 不优秀 | 合计 |
| 优秀 | 6 | 2 | 8 |
| 不优秀 | 2 | 10 | 12 |
| 合计 | 8 | 12 | 20 |
因为观测值对应的数值为0.005,
所以有99.5%的把握认为学生的数学成绩与物理成绩之间有关系.
(Ⅱ)记数学、物理成绩均优秀的6名学生为A、B、C、D、E、F,现从中选2名学生进行自主招生培训,所有的事件总数为:${C}_{6}^{2}$=15种.
A、B两人中至少有一人被选中共有:${C}_{2}^{2}$+${C}_{2}^{1}{C}_{4}^{1}$=9.
A、B两人中至少有一人被选中的概率:$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了列出2×2列联表以及独立性检验的应用问题,古典概型概率的求法,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.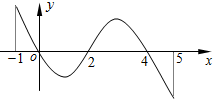 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:
f(x)的导函数y=f′(x)的图象如图所示:
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
⑤函数y=f(x)-a的零点个数可能为0,1,2,3,4.
其中正确命题的个数是( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
⑤函数y=f(x)-a的零点个数可能为0,1,2,3,4.
其中正确命题的个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
16.已知函数f(x)=e|x|+x2,且f(3a-2)>f(a-1),则实数a的取值范围为( )
| A. | (0,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
10.计算$\frac{{a}^{2}}{\sqrt{a}•\root{3}{{a}^{2}}}$的结果为( )
| A. | a${\;}^{\frac{3}{2}}$ | B. | a${\;}^{\frac{1}{6}}$ | C. | a${\;}^{\frac{5}{6}}$ | D. | a${\;}^{\frac{6}{5}}$ |
 如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.