题目内容
18．设集合A={y|y=sinx，x∈R}，B={x|y=lg（-x）}，则A∩B=（ ）| A． | （0，1] | B． | [-1，0） | C． | [-1，0] | D． | （-∞，1] |
分析 先分别求出集合A和B，由此能求出A∩B．
解答 解：∵集合A={y|y=sinx，x∈R}={y|-1≤y≤1}，
B={x|y=lg（-x）}={x|x＜0}，
∴A∩B={x|-1≤x＜0}=[-1，0）．
故选：B．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集性质的合理运用．
练习册系列答案
相关题目
如图所示，图中曲线方程为y=x2-1，则围成封闭图形（阴影部分）的面积是2．
9．
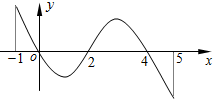已知函数f（x）的定义域为[-1，5]，部分对应值如表：
f（x）的导函数y=f′（x）的图象如图所示：
下列关于函数f（x）的命题：
①函数y=f（x）是周期函数；
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
⑤函数y=f（x）-a的零点个数可能为0，1，2，3，4．
其中正确命题的个数是（ ）
已知函数f（x）的定义域为[-1，5]，部分对应值如表：| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
下列关于函数f（x）的命题：
①函数y=f（x）是周期函数；
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
⑤函数y=f（x）-a的零点个数可能为0，1，2，3，4．
其中正确命题的个数是（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
如图，正四棱锥P-ABCD中底面边长为2$\sqrt{2}$，侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$．
10．计算$\frac{{a}^{2}}{\sqrt{a}•\root{3}{{a}^{2}}}$的结果为（ ）
| A． | a${\;}^{\frac{3}{2}}$ | B． | a${\;}^{\frac{1}{6}}$ | C． | a${\;}^{\frac{5}{6}}$ | D． | a${\;}^{\frac{6}{5}}$ |
7．在空间直角坐标系中，点A（-4，-1，-9）与点B（-10，1，-6）的距离是（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
8．某几何体的三视图如图，则几何体的体积为（ ）
| A． | 8π-16 | B． | 8π+16 | C． | 16π-8 | D． | 8π+8 |