题目内容
14．已知x，y∈R，命题p：若x＞|y|，则x＞y；命题q：若x+y＞0，则x2＞y2，在命题（1）p∨q；（2）（￢p）∧（￢q）；（3）p∧（￢q）；（4）p∧q中，证明题的个数为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 分析出命题p，q的真假，进而根据复合命题真假判断的真值表，得到答案．
解答 解：命题p：若x＞|y|，则x＞y为真命题，
若x=-1，y=2，则x+y＞0，但x2＜y2，故命题q为假命题，
故（1）p∨q为真命题；
（2）（￢p）∧（￢q）为假命题；
（3）p∧（￢q）为真命题；
（4）p∧q为假命题；
故选：B．
点评 本题以命题的真假判断与应用为载体，考查了复合命题，不等式与不等关系等知识点，难度中档．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
9．
已知函数f（x）的定义域为[-1，5]，部分对应值如表：
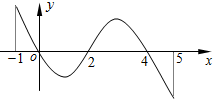
f（x）的导函数y=f′（x）的图象如图所示：
下列关于函数f（x）的命题：
①函数y=f（x）是周期函数；
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
⑤函数y=f（x）-a的零点个数可能为0，1，2，3，4．
其中正确命题的个数是（ ）
已知函数f（x）的定义域为[-1，5]，部分对应值如表：| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
下列关于函数f（x）的命题：
①函数y=f（x）是周期函数；
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
⑤函数y=f（x）-a的零点个数可能为0，1，2，3，4．
其中正确命题的个数是（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |