题目内容
19.若曲线y=$\sqrt{4x-{x}^{2}}$与直线y=$\frac{3}{4}$x+b有公共点,则b的取值范围是-3≤b≤1.分析 曲线y=$\sqrt{4x-{x}^{2}}$即(x-2)2+y2=4(y≥0),表示以A(2,0)为圆心,以2为半径的一个半圆,由圆心到直线y=$\frac{3}{4}$x+b的距离等于半径2,解得b.当直线过点(4,0)时,b=-3,可得b的范围.
解答 解:曲线y=$\sqrt{4x-{x}^{2}}$即(x-2)2+y2=4(y≥0),表示以A(2,0)为圆心,以2为半径的一个半圆,
由圆心到直线y=$\frac{3}{4}$x+b的距离等于半径2,可得$\frac{|\frac{3}{2}+b|}{\sqrt{\frac{9}{16}+1}}$=2,
∴b=1,或b=-2.
当直线过点(4,0)时,b=-3,
∵曲线y=$\sqrt{4x-{x}^{2}}$与直线y=$\frac{3}{4}$x+b有公共点,
∴可得-3≤b≤1.
故答案为:-3≤b≤1.
点评 本题的考点是直线与圆的位置关系,主要考查直线和圆的位置关系,点到直线的距离公式,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
9.下列四个命题,其中m,n,l为直线,α,β为平面
①m?α,n?α,m∥β,n∥β⇒α∥β;
②设l是平面α内任意一条直线,且l∥β⇒α∥β;
③若α∥β,m?α,n?β⇒m∥n;
④若α∥β,m?α⇒m∥β.
其中正确的是( )
①m?α,n?α,m∥β,n∥β⇒α∥β;
②设l是平面α内任意一条直线,且l∥β⇒α∥β;
③若α∥β,m?α,n?β⇒m∥n;
④若α∥β,m?α⇒m∥β.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①②④ |
10.设命题p:函数y=sin2x的最小正周期为$\frac{π}{2}$,命题q:函数y=cosx的图象关于点(π,0)中心对称,则下列判断正确的是( )
| A. | p为真 | B. | q为真 | C. | p∧q为假 | D. | p∨q为真 |
4.分别在区间[0,$\frac{π}{2}$]和[0,1]内任取两个实数x,y,则不等式y≤cosx恒成立的概率为( )
| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{1}{2}$ |
11.下列命题正确的是( )
| A. | 经过三点确定一个平面 | |
| B. | 经过一条条直线和一个点确定一个平面 | |
| C. | 梯形确定一个平面 | |
| D. | 四边形确定一个平面 |
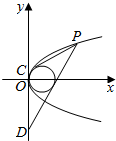 斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.
斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.