题目内容
8.化简与求值:(1)化简:$\frac{1+tan15°}{1-tan15°}$;
(2)已知α,β都是锐角,cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,求cosβ的值.
分析 (1)由条件利用两角和的正切公式,求得要求式子的值.
(2)由条件利用同角三角函数的基本关系求得sinα、sin(α+β)的值,再利用两角差的余弦公式求得cosβ的值.
解答 解:(1)$\frac{1+tan15°}{1-tan15°}$=$\frac{tan45°+tan15°}{1-tan45°•tan15°}$=tan(45°+15°)=tan60°=$\sqrt{3}$.
(2)∵已知α,β都是锐角,cosα=$\frac{1}{7}$,∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{4\sqrt{3}}{7}$,
∵cos(α+β)=-$\frac{11}{14}$,∴α+β为钝角,sin(α+β)=$\sqrt{{1-cos}^{2}(α+β)}$=$\frac{5\sqrt{3}}{14}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-$\frac{11}{14}$•$\frac{1}{7}$+$\frac{4\sqrt{3}}{7}$•$\frac{5\sqrt{3}}{14}$=$\frac{1}{2}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的三角公式的应用,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
3.已知α=-$\frac{55π}{6}$,则α所在的象限的是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知数列{an}满足a4=23,an+1=2an+1,则a2等于( )
| A. | 5 | B. | $\frac{11}{2}$ | C. | 6 | D. | $\frac{13}{2}$ |
18.已知指数函数y=(2a-1)x在(1,+∞)上是减函数,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | (1,+∞) | C. | (-∞,1) | D. | [1,+∞) |
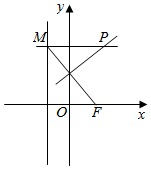 在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.
在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.