题目内容
9.下列四个命题,其中m,n,l为直线,α,β为平面①m?α,n?α,m∥β,n∥β⇒α∥β;
②设l是平面α内任意一条直线,且l∥β⇒α∥β;
③若α∥β,m?α,n?β⇒m∥n;
④若α∥β,m?α⇒m∥β.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①②④ |
分析 利用空间线面、面面平行的性质定理和判定定理分别分析选择.
解答  解:在长方体ABCD-A1B1C1D1中,
解:在长方体ABCD-A1B1C1D1中,
①若平面AC是平面α,平面A1C1是平面β,
直线AD是直线m,A1B1是直线n,
显然满足m?α,n?α,m∥β,n∥β,但是α与β相交,不正确;
②若平面α内任意一条直线平行于平面β,则平面α的两条相交直线平行于平面β,满足面面平行的判定定理,所以α∥β;故正确
③若平面AC是平面α,平面BC1是平面β,
直线AD是直线m,点E,F分别是AB,CD的中点,则EF∥AD,EF是直线n,
显然满足α∥β,m?α,n?β,但是m与n异面,不正确;
④由面面平行结合线面平行的定义可得m∥β,正确,
故选:C.
点评 本题考查了空间线面、面面平行的性质定理和判定定理的运用判断面面关系、线面关系;关键是熟练掌握有关的定理.

练习册系列答案
相关题目
14.如表提供了某新生婴儿成长过程中时间x(月)与相应的体重y(公斤)的几组对照数据.
(1)如y与x具有较好的线性关系,请根据表中提供的数据,求出线性回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)由此推测当婴儿生长到五个月时的体重为多少?
参考公式:$\stackrel{∧}{y}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$;$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=27.5.
| x | 0 | 1 | 2 | 3 |
| y | 3 | 3.5 | 4.5 | 5 |
(2)由此推测当婴儿生长到五个月时的体重为多少?
参考公式:$\stackrel{∧}{y}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$;$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=27.5.
1.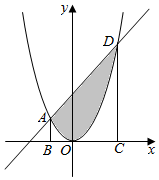 如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )
如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )
 如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )
如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
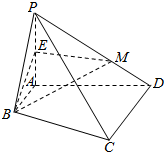 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.