题目内容
9.已知函数y=f(x)+x是偶函数,且f(3)=1,则f(-3)=7.分析 根据函数奇偶性的性质,建立方程关系进行求解即可.
解答 解:∵函数y=f(x)+x是偶函数,
∴f(-x)-x=f(x)+x,
即f(-x)=f(x)+2x,
∵f(3)=1,
∴f(-3)=f(3)+2×3=1+6=7,
故答案为:7.
点评 本题主要考查函数值的计算,根据函数奇偶性的性质建立方程公式是解决本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
4.在等腰直角三角形ABC中,AB=AC=1,点E为斜边BC的中点,点M在线段AB上运动,则($\overline{AE}$-$\overline{AM}$)•($\overline{AC}$-$\overline{AM}$)的取值范围是( )
| A. | [$\frac{7}{16}$,$\frac{1}{2}$] | B. | [$\frac{7}{16}$,1] | C. | [$\frac{1}{2}$,1] | D. | [0,1] |
14.不等式$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$≤2$\sqrt{6}$的解集为( )
| A. | {x|-$\sqrt{2}$≤x≤$\sqrt{2}$} | B. | {x|-$\sqrt{3}$≤x≤$\sqrt{3}$} | C. | {x|-2≤x≤2} | D. | {x|-$\sqrt{5}$≤x≤$\sqrt{5}$} |
18.已知指数函数y=(2a-1)x在(1,+∞)上是减函数,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | (1,+∞) | C. | (-∞,1) | D. | [1,+∞) |
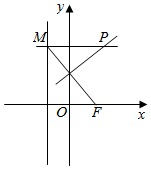 在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.
在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.