设命题p:函数y=sin2x的最小正周期为$\frac{π}{2}$.命题q:函数y=cosx的图象关于点中心对称.则下列判断正确的是( )A．p为真B．q为真C．p∧q为假D．p∨q为真题目和参考答案——青夏教育精英家教网—

题目内容

10．设命题p：函数y=sin2x的最小正周期为$\frac{π}{2}$，命题q：函数y=cosx的图象关于点（π，0）中心对称，则下列判断正确的是（　　）

A．

p为真

B．

q为真

C．

p∧q为假

D．

p∨q为真

分析由题设条件可先判断出两个命题的真假，再根据复合命题真假的判断规则判断出选项中复合命题的真假即可得出正确选项．

解答解：由于函数y=sin2x的最小正周期为π，故命题p是假命题；
函数y=cosx的图象关于直线x=kπ对称，k∈Z，故q是假命题；
结合复合命题的判断规则知：p∧q为假命题，p∨q为是假命题；
故选：C．

点评本题考查复合命题的真假判断，解题的关键是正确判断所涉及命题的真假及熟练掌握复合命题的真假判断规则，本题属于高考常考题型也是对命题考查的常规题型，知识性强，难度不大．

练习册系列答案

1．

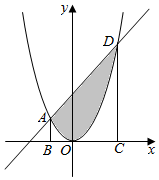如图所示，直线x-y+2=0与抛物线y=x²相交于A，D两点，分别过A，D作平行于y轴的直线交x轴于B，C两点，随机向梯形ABCD内投一点P，则点P落在抛物线弓形AOD内（图中阴影部分）的概率是（　　）

18．设f（x）是定义在R上且周期为2的函数，在区间[-1，1]上，f（x）=$\left\{\begin{array}{l}{ax，-1≤x＜0}\\{\frac{bx+2}{x+1}，0≤x≤1}\end{array}\right.$，其中a，b∈R，若f（$\frac{1}{2}$）=f（$\frac{3}{2}$），则a+b的值（　　）

5．已知函数f（x）=log_a（x²-2x+5）（a＞0），若f（2）=$\frac{1}{lo{g}_{5}2}$，g（x）=2^x-k．
（Ⅰ）求实数a的值；
（Ⅱ）当x∈[1，3]时，记f（x），g（x）的值域分别为集合A，B，若A∩B=A，求实数k的取值范围．

15．已知命题p：2和8的等比中项是4；命题q：平面内到两个定点F₁，F₂的距离之差等于常数2a（|F₁F₂|＜2a）的点的轨迹是双曲线，则下列命题为真命题的是（　　）

2．已知△ABC内角A，B，C的对边分别是a，b，c，以下说法：
①在△ABC中，“a，b，c成等差数列”是“acos²$\frac{C}{2}$+ccos²$\frac{A}{2}$=$\frac{3}{2}$b”的充要条件；
②命题“在锐角三角形ABC中，sinA＞cosB”的逆命题和逆否命题均为真命题；
③命题“对任意三角形ABC，sinA+sinB＞sinC”为假命题．
正确的个数为（　　）

19．若曲线y=$\sqrt{4x-{x}^{2}}$与直线y=$\frac{3}{4}$x+b有公共点，则b的取值范围是-3≤b≤1．

20．

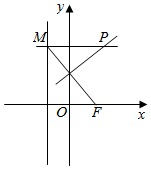在平面直角坐标系xOy中，点F（1，0），直线x=-1与动直线y=n的交点为M，线段MF的中垂线与动直线y=n的交点为P．
（Ⅰ）求点P的轨迹Г的方程；
（Ⅱ）过动点M作曲线Г的两条切线，切点分别为A，B，求证：∠AMB的大小为定值．

试题分类