题目内容
等差数列{an}中,a7=4,a19=2a9
(1)求{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Sn.
(1)求{an}的通项公式;
(2)设bn=
| 1 |
| 2nan |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)先设出等差数列{an}的公差为d,然后由等差数列的通项公式及题意列出方程,求出首项a1和公差d,进而求出数列{an}的通项公式;
(2)将(1)中所求的{an}的通项公式代入bn=
,即可求出数列{bn}的通项公式,再运用裂项相消法求出其前n项和Sn即可.
(2)将(1)中所求的{an}的通项公式代入bn=
| 1 |
| nan |
解答:
解:(1)设等差数列{an}的公差为d,
则由an=a1+(n-1)d得:
解得a1=1,d=
,
所以{an}的通项公式为an=
,
(2)因为bn=
=
=
-
,
所以Sn=(
-
)+(
-
)+…+(
-
)=
.
则由an=a1+(n-1)d得:
|
解得a1=1,d=
| 1 |
| 2 |
所以{an}的通项公式为an=
| n+1 |
| 2 |
(2)因为bn=
| 1 |
| 2nan |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以Sn=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了等差数列的通项公式,以及数列的求和方法:裂项相消法,属于中档题.

练习册系列答案
相关题目
已知集合A={1,2,3,4},B={a,b,c},f:A→B为集合A到集合B的一个函数,那么该函数的值域C的不同情况有( )
| A、7种 | B、4种 | C、8种 | D、12种 |
已知P={-1,0,
},Q={y|y=sinθ,θ∈R},则P∩∁RQ=( )
| 2 |
| A、∅ | ||
B、{
| ||
| C、{-1,0} | ||
D、{-1,0,
|
下列结论错误的是( )
| A、命题:“若a>b>0,则a2>b2”的逆命题是假命题 | ||||||||
| B、若函数f(x)可导,则f′(x0)是x0为函数极值点的必要不充分条件 | ||||||||
C、向量
| ||||||||
| D、命题p:“?x∈R,ex≥x+1”的否定是“?x∈R,ex<x+1” |
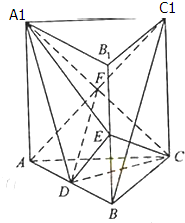 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4