题目内容
9．“（$\frac{1}{3}$）x＜1”是“$\frac{1}{x}$＞1”的（ ）| A． | 充分且不必要条件 | B． | 必要且不充分条件 | ||
| C． | 充要条件 | D． | 既非充分也非必要条件 |
分析 解不等式，根据集合的包含关系判断即可．
解答 解：由“（$\frac{1}{3}$）x＜1”，解得：x＞0，
由“$\frac{1}{x}$＞1”，解得：0＜x＜1，
故“（$\frac{1}{3}$）x＜1”是“$\frac{1}{x}$＞1”的必要不充分条件，
故选：B．
点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．
练习册系列答案
相关题目
19．
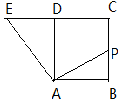如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为BC的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（ ）
如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为BC的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（ ）| A． | 3 | B． | 2 | C． | 1 | D． | $\frac{5}{2}$ |
20．直线mx-y-2=0与3x-（2+m）y-1=0平行，则实数m为（ ）
| A． | 1或-3 | B． | -1或3 | C． | -$\frac{1}{2}$ | D． | -1 |
17．已知函数f（x）定义域为R，命题：p：f（x）为奇函数，q：${∫}_{-1}^{1}$f（x）dx=0，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
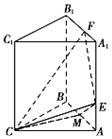在三棱柱ABC-A1B1C1中，CA=CB，侧面ABB1A1是边长为2的正方形，点E，F分别在线段AAl，A1B1上，且AE=$\frac{1}{2}$，A1F=$\frac{3}{4}$，CE⊥EF，M为AB中点