题目内容
定义行列式运算：|
|=a1a4-a2a3，将函数f（x）=|
|（ω＞0）向左平移
个单位，所得图象对应的函数为偶函数，则ω的最小值是 ．
|
|
| 5π |
| 6 |
考点：二阶行列式的定义,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值
分析：利用行列式求出函数的解析式，然后平移，得到新函数，利用函数的性质求出ω的最小值．
解答：
解：f（x）=
=
cosωx-sinωx=2cos（ωx+
），
图象向左平移
个单位，
得f（x+
）=2cos[ω（x+
）+
）]=2cos（ωx+
ω+
），
所得图象对应的函数为偶函数，∴
ω+
=kπ，k∈Z，
则当ω取得最小值为1时，函数为偶函数．
故答案为：1．
|
| 3 |
| π |
| 6 |
图象向左平移
| 5π |
| 6 |
得f（x+
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
所得图象对应的函数为偶函数，∴
| 5π |
| 6 |
| π |
| 6 |
则当ω取得最小值为1时，函数为偶函数．
故答案为：1．
点评：本题考查二阶行列式的展开法则，解题时要注意函数的平移和偶函数的合理运用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
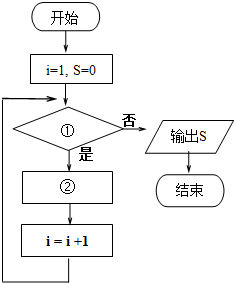已知等比数列{an}中，a1=1，公比q=2，计算数列{an}的前20项的和S，现已给出该算法的程序框图如图所示：
如图，在△ABC中，AD、BE分别是BC、AC边上的高，∠C=60°，求证：