题目内容
解关于x的不等式:ax2+ax-1<0.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:对二次项系数讨论,分a=0和a≠0两种情况分别解答.求出ax2+ax+1的判别式,通过讨论判别式的情况,求出不等式的解解集.
解答:
解:①a=0时不等式为-1<0成立,此时x∈R;
②a≠0时,因为△=a2+4a,
当a>0时,解集为(
,
);
当a=-4时,解集为{x|x≠-
};
当-4<a<0时,解集为R;
当a<-4时,△>0,不等式的解集为:(-∞,
)∪(
,+∞);
②a≠0时,因为△=a2+4a,
当a>0时,解集为(
-a-
| ||
| 2a |
-a+
| ||
| 2a |
当a=-4时,解集为{x|x≠-
| 1 |
| 2 |
当-4<a<0时,解集为R;
当a<-4时,△>0,不等式的解集为:(-∞,
-a-
| ||
| 2a |
-a+
| ||
| 2a |
点评:本题考查了一元二次不等式的解法以及讨论思想的运用;关键是准确分类做到不重不漏.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
若点O是△ABC的外心,且
+
+
=
,则△ABC的内角C为( )
| OA |
| OB |
| CO |
| 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为
对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为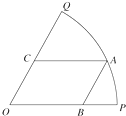 地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=
地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=